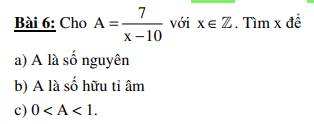Lời giải:
a. Với $x$ nguyên $\Rightarrow x-10$ là số nguyên.
Khi đó, để $A=\frac{7}{x-10}$ nguyên thì $7\vdots x-10$
$\Rightarrow x-10\in\left\{-1; 1; 7; -7\right\}$
$\Rightarrow x\in\left\{9; 11; 17; 3\right\}$
b. Vì $x-10$ nguyên với mọi $x$ nguyên nên $A$ luôn là số hữu tỉ
Để $A<0\Leftrightarrow \frac{7}{x-10}<0$
$\Leftrightarrow x-10<0$
$\Leftrightarrow x<10$
c.
$0< A\Leftrightarrow 0< \frac{7}{x-10}\Leftrightarrow 0< x-10$
$\Leftrightarrow x>10(1)$
$A< 1\Leftrightarrow \frac{7}{x-10}< 1\Leftrightarrow \frac{7}{x-10}-1<0$
$\Leftrightarrow \frac{17-x}{x-10}<0$
$\Leftrightarrow 17-x< 0$ (do $x-10>0$ theo $(1)$)
$\Leftrightarrow x> 17$
Vậy $x>17$.