\(B=\sqrt{4+\sqrt{10+2\sqrt{5}}}+\sqrt{4-\sqrt{10+2\sqrt{5}}}\)
\(\Leftrightarrow B^2=4+\sqrt{10+2\sqrt{5}}+4-\sqrt{10+2\sqrt{5}}+2\sqrt{\left(4+\sqrt{10+2\sqrt{5}}\right)\left(4-\sqrt{10+2\sqrt{5}}\right)}\)
\(\Leftrightarrow B^2=8+2\sqrt{4^2-\left(\sqrt{10+2\sqrt{5}}\right)^2}\)
\(\Leftrightarrow B^2=8+2\sqrt{16-10-2\sqrt{5}}\) ( vì \(10+2\sqrt{5}>0\) )
\(\Leftrightarrow B^2=8+2\sqrt{6-2\sqrt{5}}\)
\(\Leftrightarrow B^2=8+2\sqrt{\left(\sqrt{5}-1\right)^2}\)
\(\Leftrightarrow B^2=8+2.\left|\sqrt{5}-1\right|\)
\(\Leftrightarrow B^2=8+2.\left(\sqrt{5}-1\right)\) ( vì \(\sqrt{5}>1\) )
\(\Leftrightarrow B^2=8+2\sqrt{5}-2\)
\(\Leftrightarrow B^2=6+2\sqrt{5}\)
\(\Leftrightarrow B^2=\left(\sqrt{5}+1\right)^2\)
\(\Leftrightarrow\left|B\right|=\left|\sqrt{5}+1\right|\)
\(\Leftrightarrow B=\sqrt{5}+1\) ( vì `B` dương )
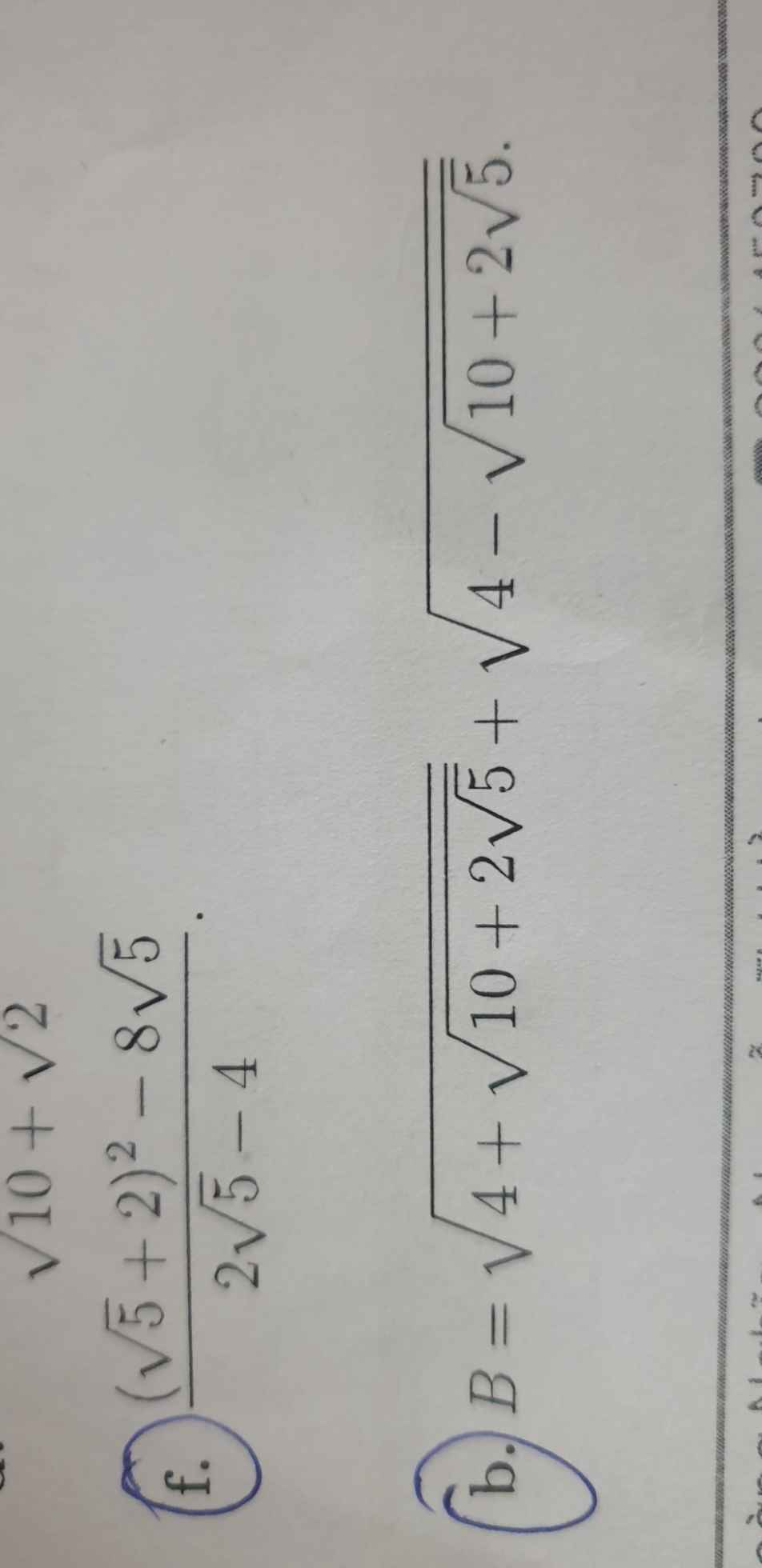
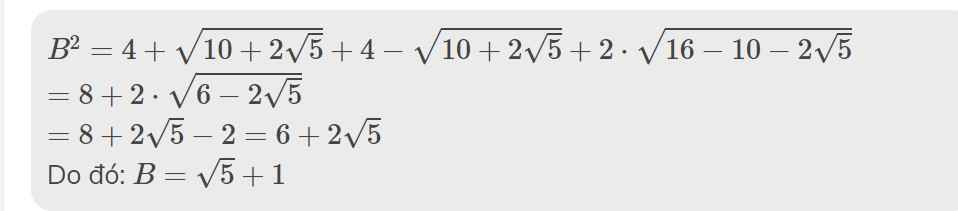
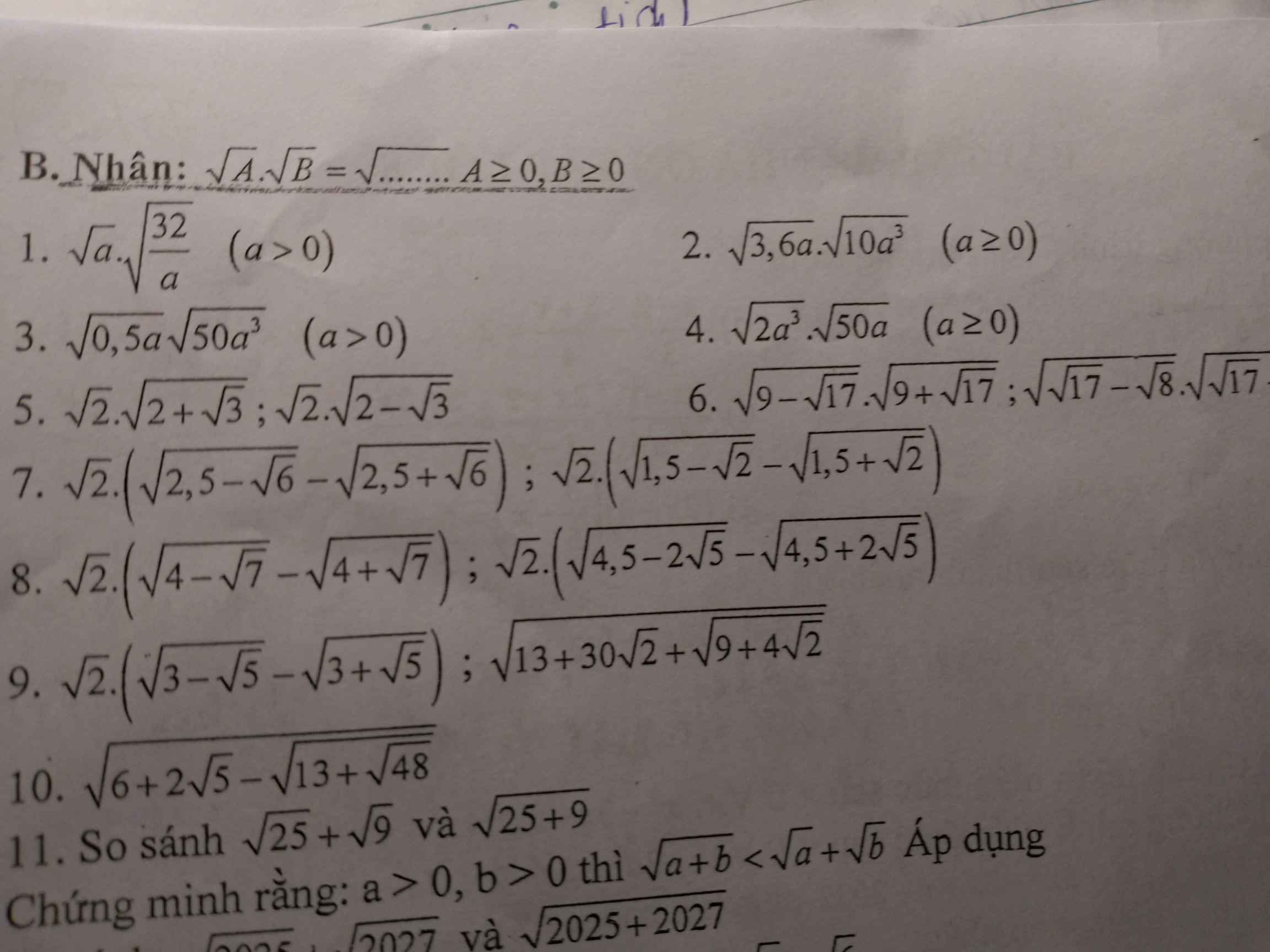
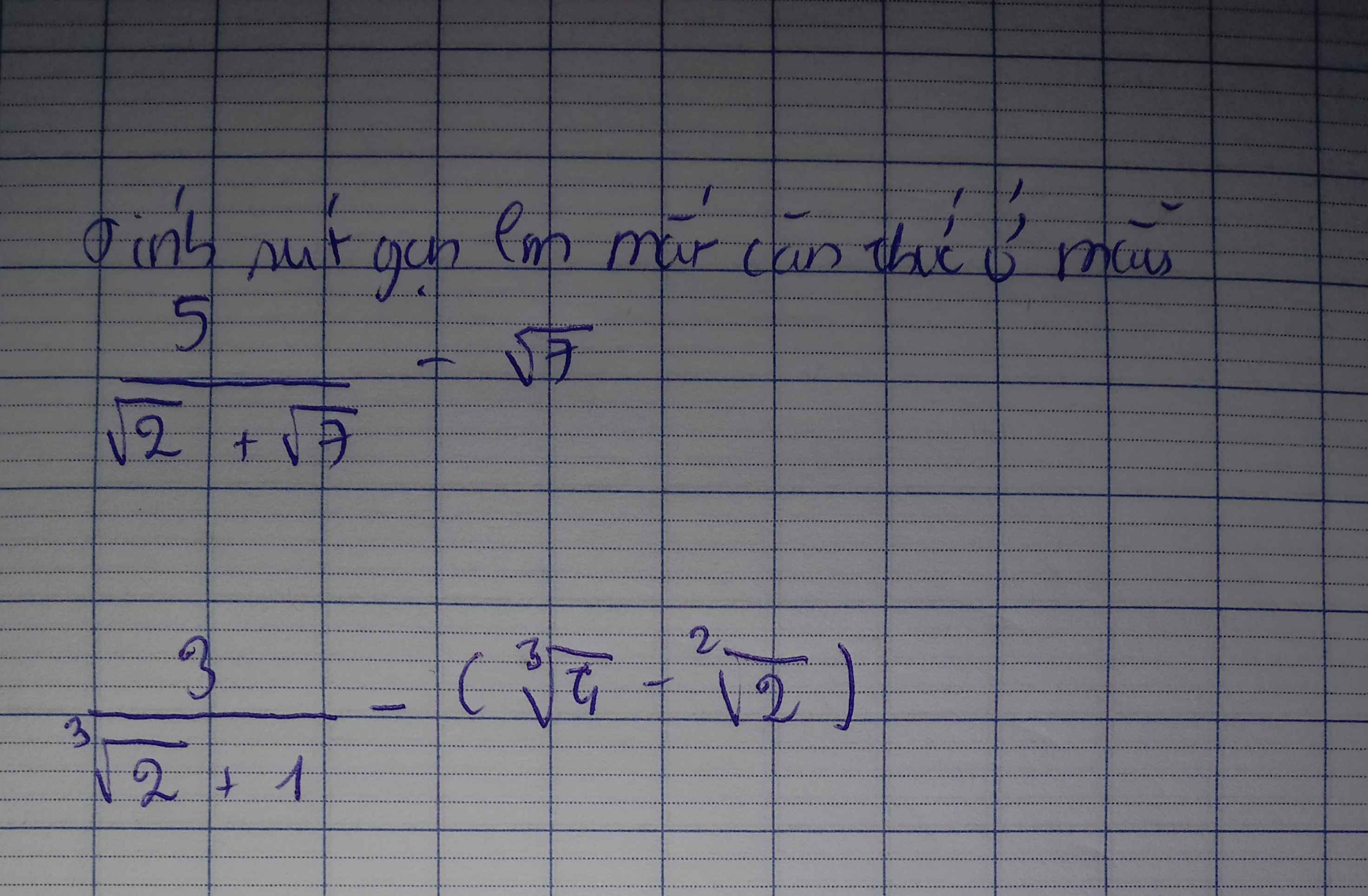
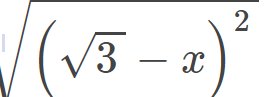
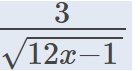GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ
