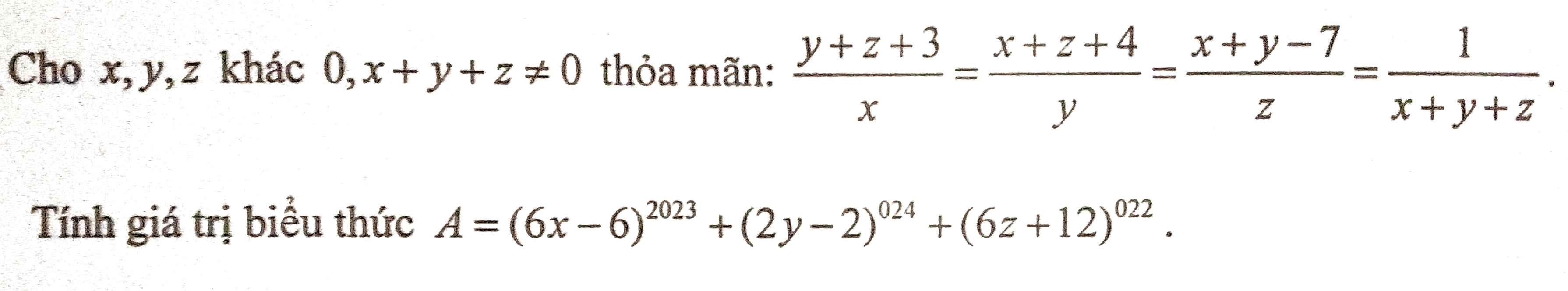\(\dfrac{y+z+3}{x}=\dfrac{x+z+4}{y}=\dfrac{x+y-7}{z}=\dfrac{y+z+3+x+z+4+x+y-7}{x+y+z}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2\)
\(\Rightarrow\dfrac{1}{x+y+z}=2\Rightarrow x+y+z=\dfrac{1}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{y+z+3}{x}=\dfrac{\dfrac{1}{2}-x+3}{x}=2\\\dfrac{z+z+4}{y}=\dfrac{\dfrac{1}{2}-y+4}{y}=2\\\dfrac{x+y-7}{z}=\dfrac{\dfrac{1}{2}-z-7}{z}=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}.\dfrac{1}{3}=\dfrac{5}{6}\\y=\dfrac{9}{2}.\dfrac{1}{3}=\dfrac{3}{2}\\z=\dfrac{\left(-13\right)}{2}.\dfrac{1}{3}=-\dfrac{13}{6}\end{matrix}\right.\)
\(\Rightarrow A=\left(6.\dfrac{7}{6}-6\right)^{2023}+\left(2.\dfrac{3}{2}-2\right)^{2024}+\left(6.\left(\dfrac{-13}{6}\right)+12\right)^{2022}=1^{2023}+1^{2024}+\left(-1\right)^{2022}=3\)