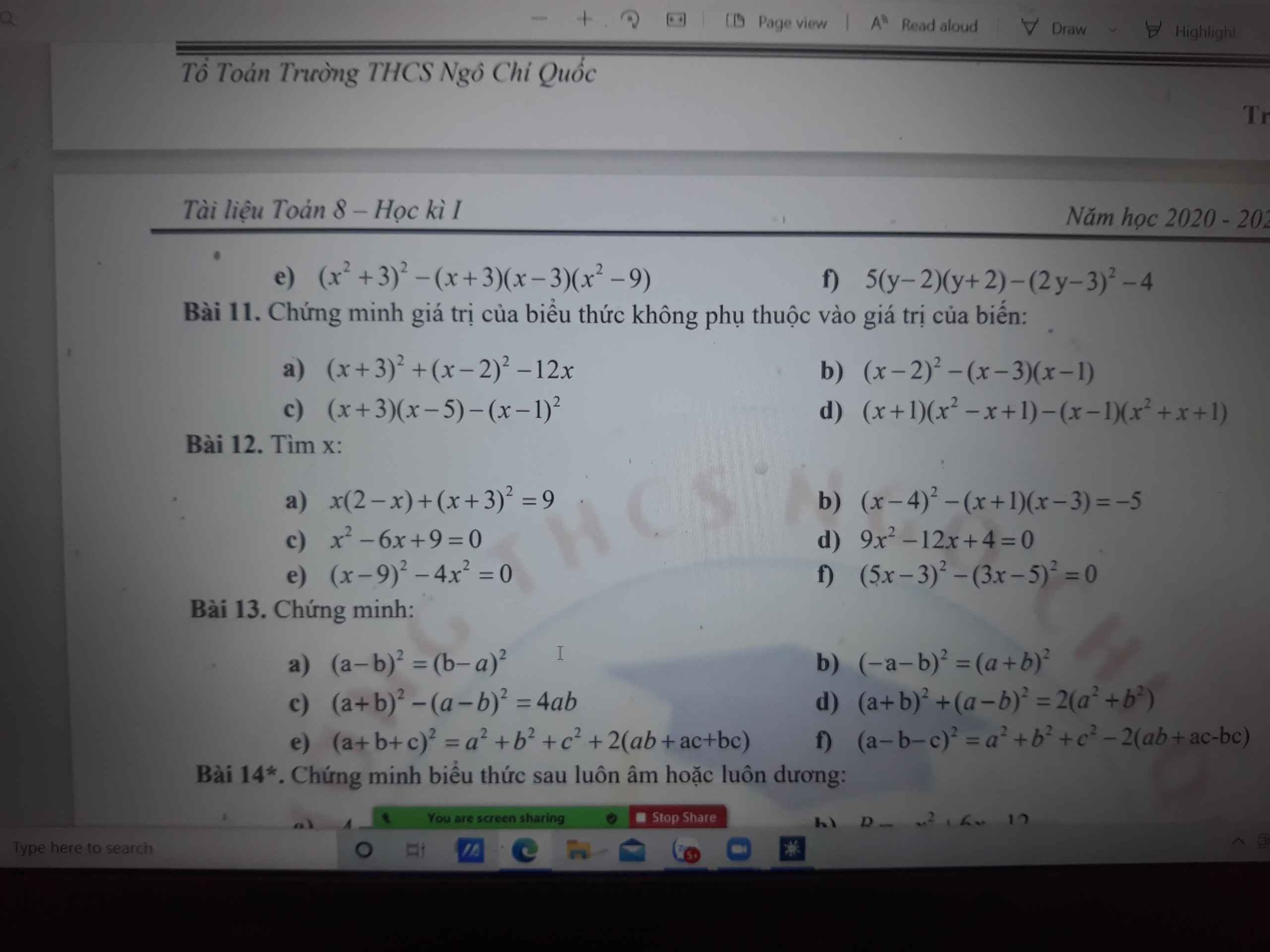
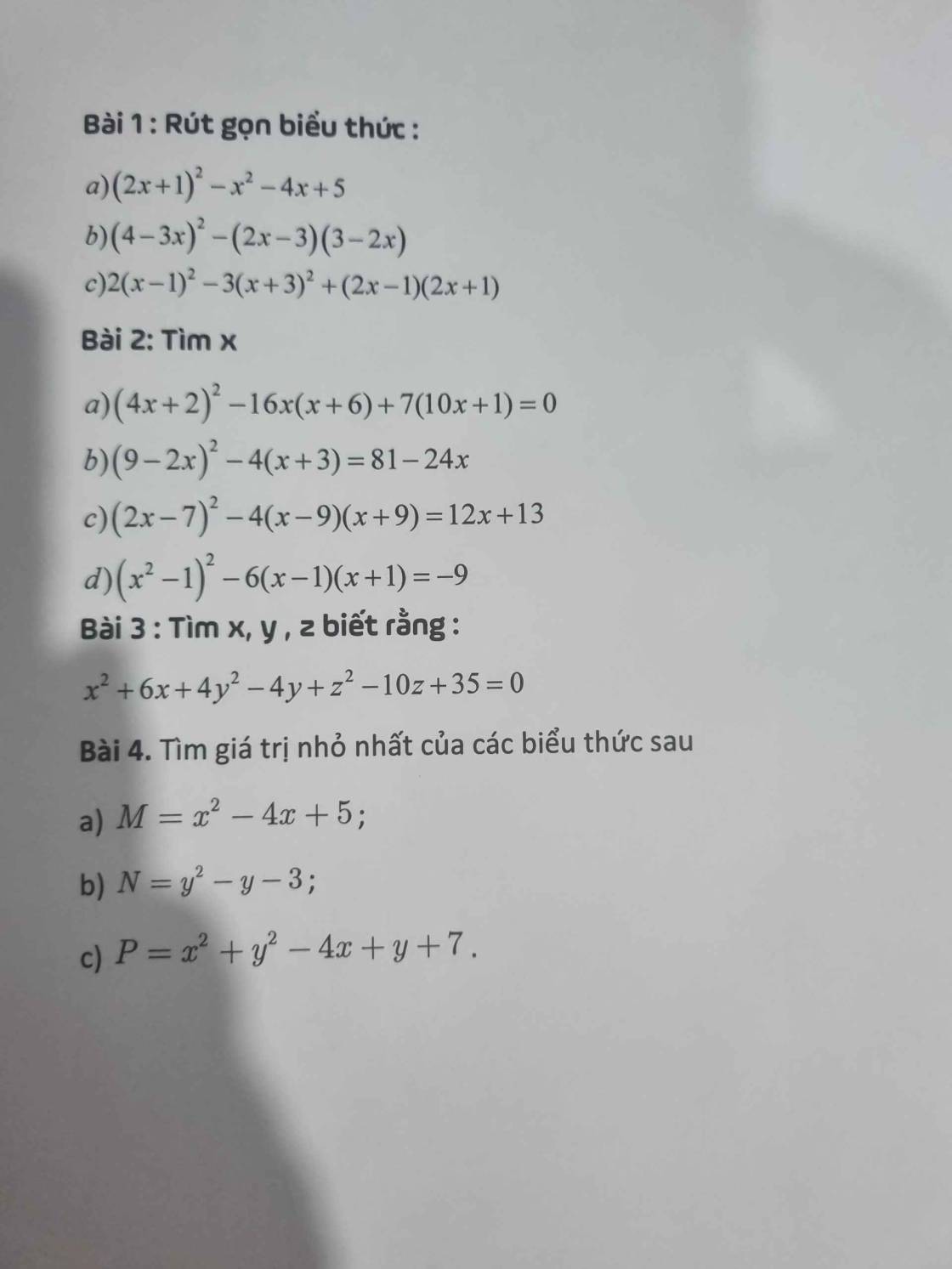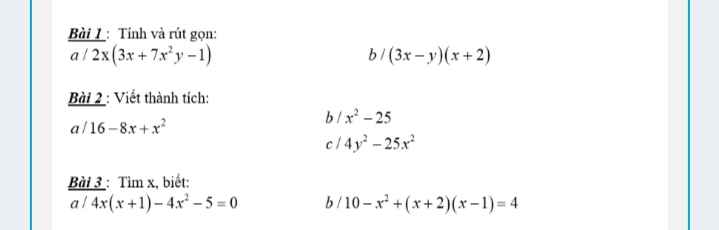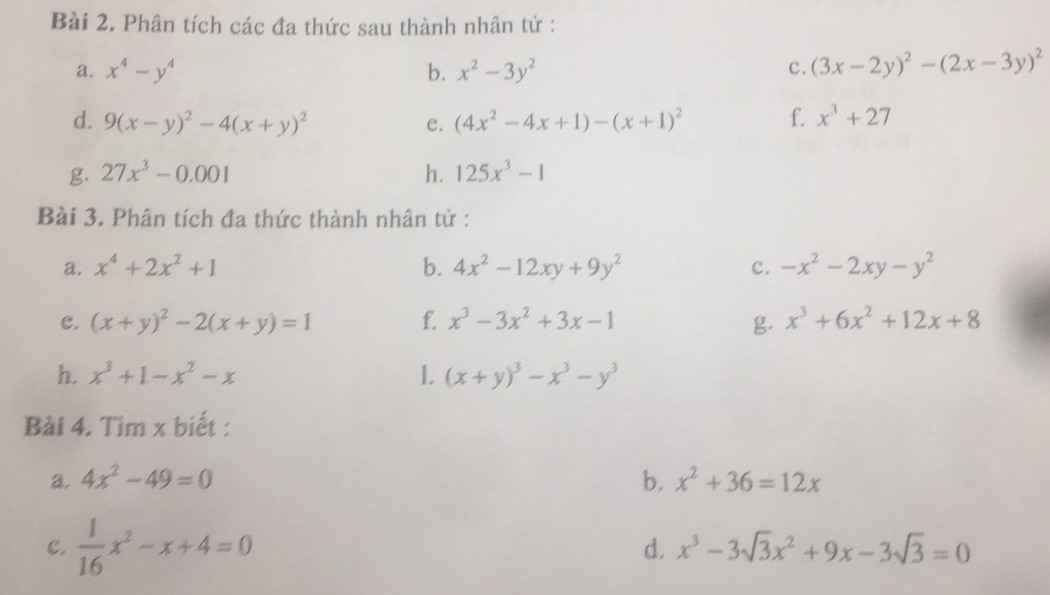Bài 3.4\(12\left(5^2+1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)=\dfrac{24\left(5^2+1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)}{2}=\dfrac{\left(5^2-1\right)\left(5^2+1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)}{2}=\dfrac{\left(5^4-1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)}{2}=\dfrac{\left(5^8-1\right)\left(5^8+1\right)\left(5^{16}+1\right)}{2}=\dfrac{\left(5^{16}-1\right)\left(5^{16}+1\right)}{2}=\dfrac{5^{32}-1}{2}\)
Bài 3.5
\(\left(a+b+c\right)^3=\left(a+b\right)^3+3\left(a+b\right)^2c+3\left(a+b\right)c^2+c^3=a^3+3a^2b+3ab^2+b^3+c^3+3\left(a+b\right)\left(ac+bc+c^2\right)=a^3+b^3+c^3+3\left(a+b\right)\left(ab+bc+ac+c^2\right)=a^3+b^3+c^3+3\left(a+b\right)\left[b\left(a+c\right)+c\left(a+c\right)\right]=a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
3.4.
P=12(52+1)(54+1)(58+1)(516+1)=1/2(532-1)