1.
\(SA\perp\left(ABC\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABC)
\(\Rightarrow\widehat{SCA}=\left(SC;\left(ABC\right)\right)\)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=2\Rightarrow\widehat{SCA}\approx63^026'\)
2.
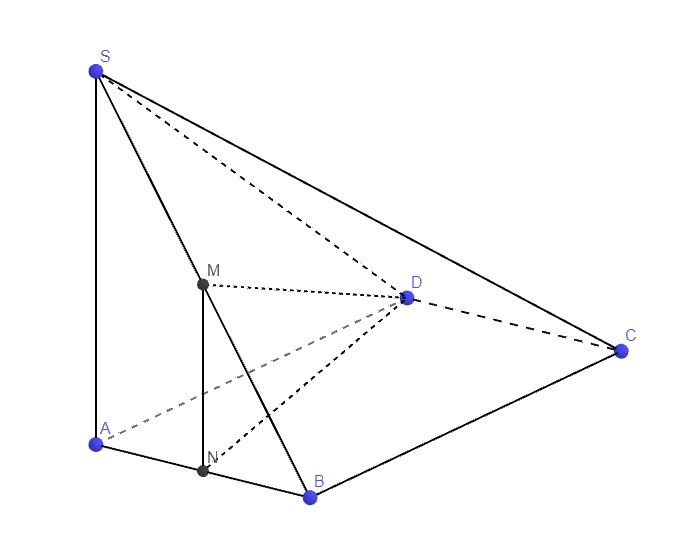
\(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}=\left(SC;\left(ABCD\right)\right)\)
\(AC=\sqrt{AB^2+AD^2}=a\sqrt{5}\)
\(SA=\sqrt{SB^2-AB^2}=a\sqrt{3}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=\sqrt{\dfrac{3}{5}}\Rightarrow\widehat{SCA}\approx37^046'\)
b.
Gọi N là trung điểm AB \(\Rightarrow MN\) là đường trung bình tam giác SAB
\(\Rightarrow MN||SA\Rightarrow MN\perp\left(ABCD\right)\)
\(\Rightarrow DN\) là hình chiếu vuông góc của DM lên (ABCD)
\(\Rightarrow\widehat{MDN}=\left(DM;\left(ABCD\right)\right)\)
\(MN=\dfrac{1}{2}SA=\dfrac{a\sqrt{3}}{2}\); \(DN=\sqrt{AD^2+AN^2}=\sqrt{AD^2+\left(\dfrac{AB}{2}\right)^2}=\dfrac{a\sqrt{17}}{2}\)
\(\Rightarrow tan\widehat{MDN}=\dfrac{MN}{DN}=\dfrac{\sqrt{51}}{17}\Rightarrow\widehat{MDN}\approx22^047'\)
3.
a.
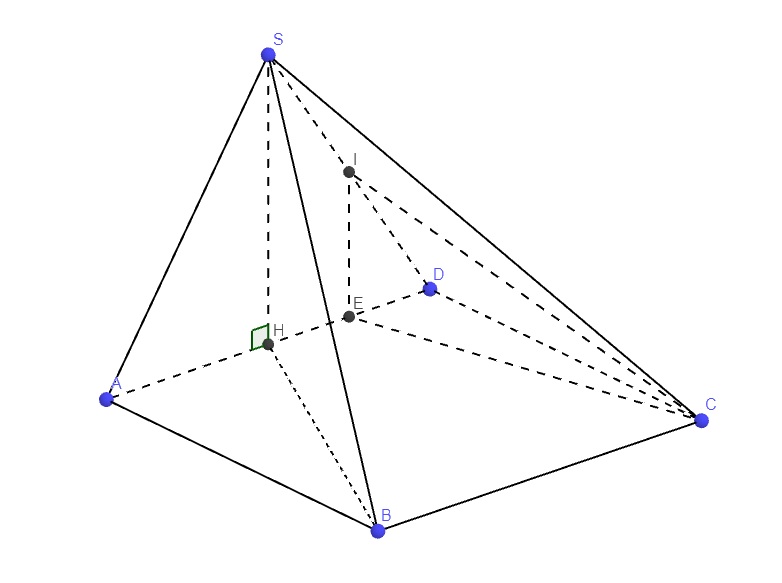
\(SH\perp\left(ABCD\right)\Rightarrow DH\) là hình chiếu vuông góc của SD lên (ABCD)
\(\Rightarrow\widehat{SDH}=\left(SD;\left(ABCD\right)\right)\)
\(AH=DH=\dfrac{AD}{2}=a\)
\(SH=\sqrt{SA^2-AH^2}=2a\)
\(\Rightarrow tan\widehat{SDH}=\dfrac{SH}{DH}=2\Rightarrow\widehat{SDH}\approx63^026'\)
b.
\(SH\perp\left(ABCD\right)\Rightarrow\) BH là hcvg của SB lên (ABCD)
\(\Rightarrow\widehat{SBH}=\left(SB;\left(ABCD\right)\right)\)
\(BH=\sqrt{AB^2+AH^2}=a\sqrt{5}\)
\(\Rightarrow tan\widehat{SBH}=\dfrac{SH}{BH}=\dfrac{2}{\sqrt{5}}\Rightarrow\widehat{SBH}\approx41^048'\)
c.
Gọi E là trung điểm DH \(\Rightarrow IE\) là đường trung bình tam giác SDH
\(\Rightarrow IE||SH\Rightarrow IE\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{ICE}=\left(CI;\left(ABCD\right)\right)\)
\(IE=\dfrac{1}{2}SH=a\) ; \(CE=\sqrt{CD^2+DE^2}=\sqrt{CD^2+\left(\dfrac{DH}{2}\right)^2}=\dfrac{a\sqrt{17}}{2}\)
\(\Rightarrow tan\widehat{ICE}=\dfrac{IE}{CE}=\dfrac{2}{\sqrt{17}}\Rightarrow\widehat{ICE}\approx25^052'\)


















 p nào làm giúp mk với ạ
p nào làm giúp mk với ạ