Câu 5:
\(C^k_n=C^{n-k}_n\)
=>\(C^0_{2011}+C^1_{2011}+...+C^{1005}_{2011}=C^{1006}_{2011}+C^{1007}_{2011}+...+C^{2010}_{2011}+C^{2011}_{2011}\)
=>\(A=C^0_{2011}+C^1_{2011}+...+C^{1005}_{2011}=\left(C^0_{2011}+C^1_{2011}+...+C^{2011}_{2011}\right)\cdot\dfrac{1}{2}=\dfrac{B}{2}\)
B là tổng các hệ số của khai triển (x+1)^2011
Khi x=1 thì (1+1)^2011=2^2011
=>B=2^2011
=>A=2^2011/2=2^2010
Đúng 0
Bình luận (0)
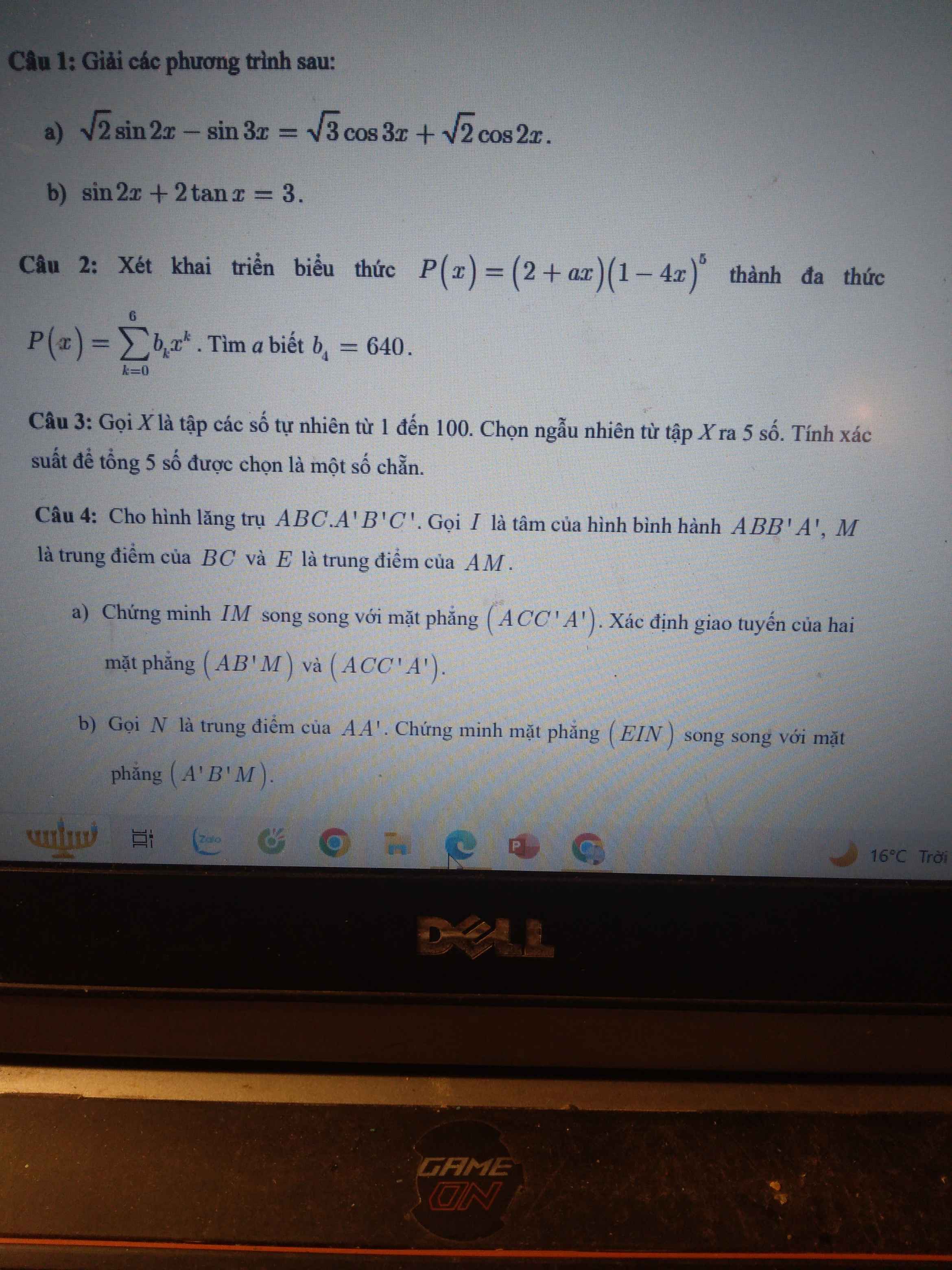
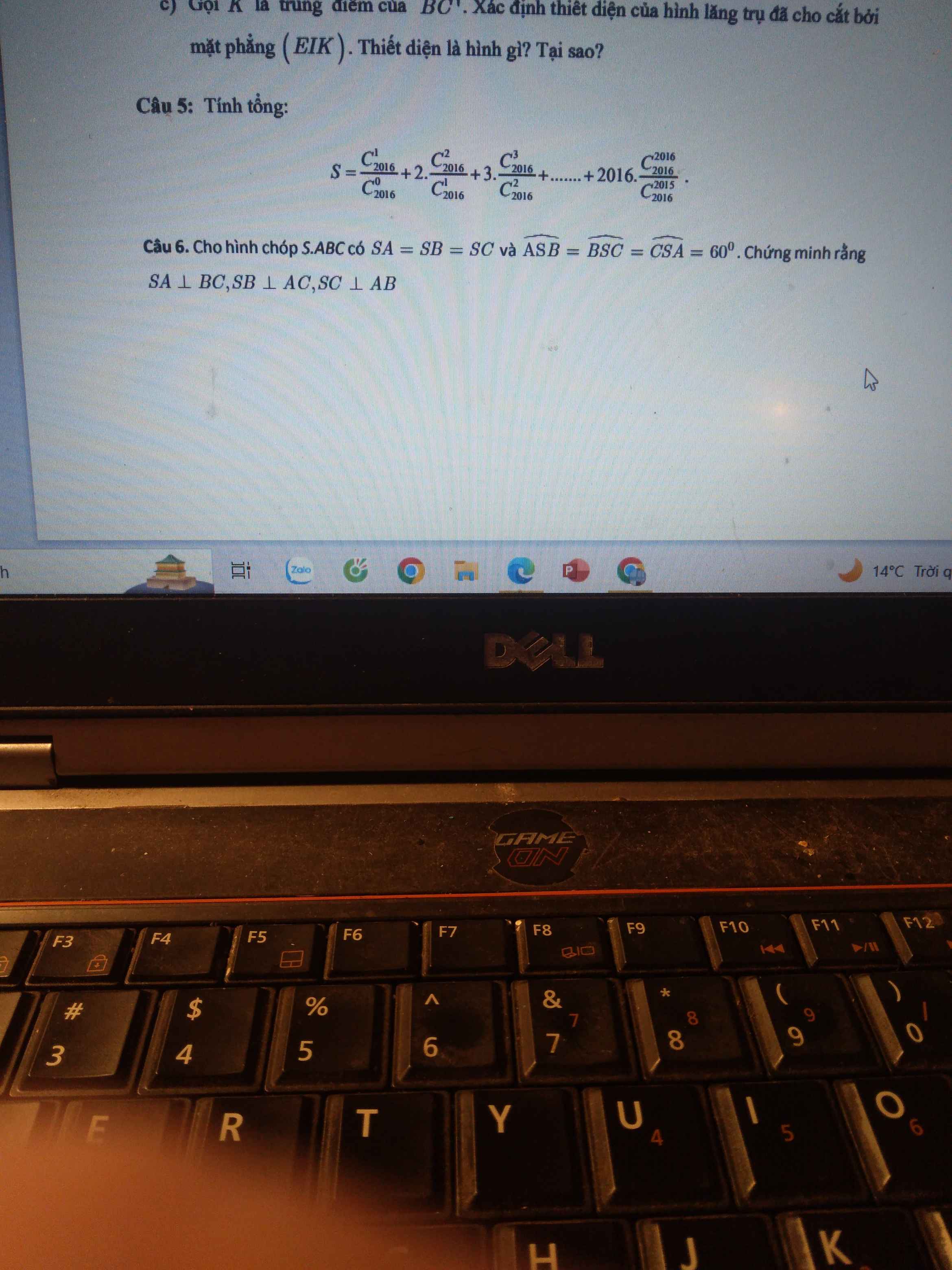
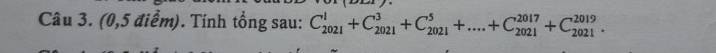
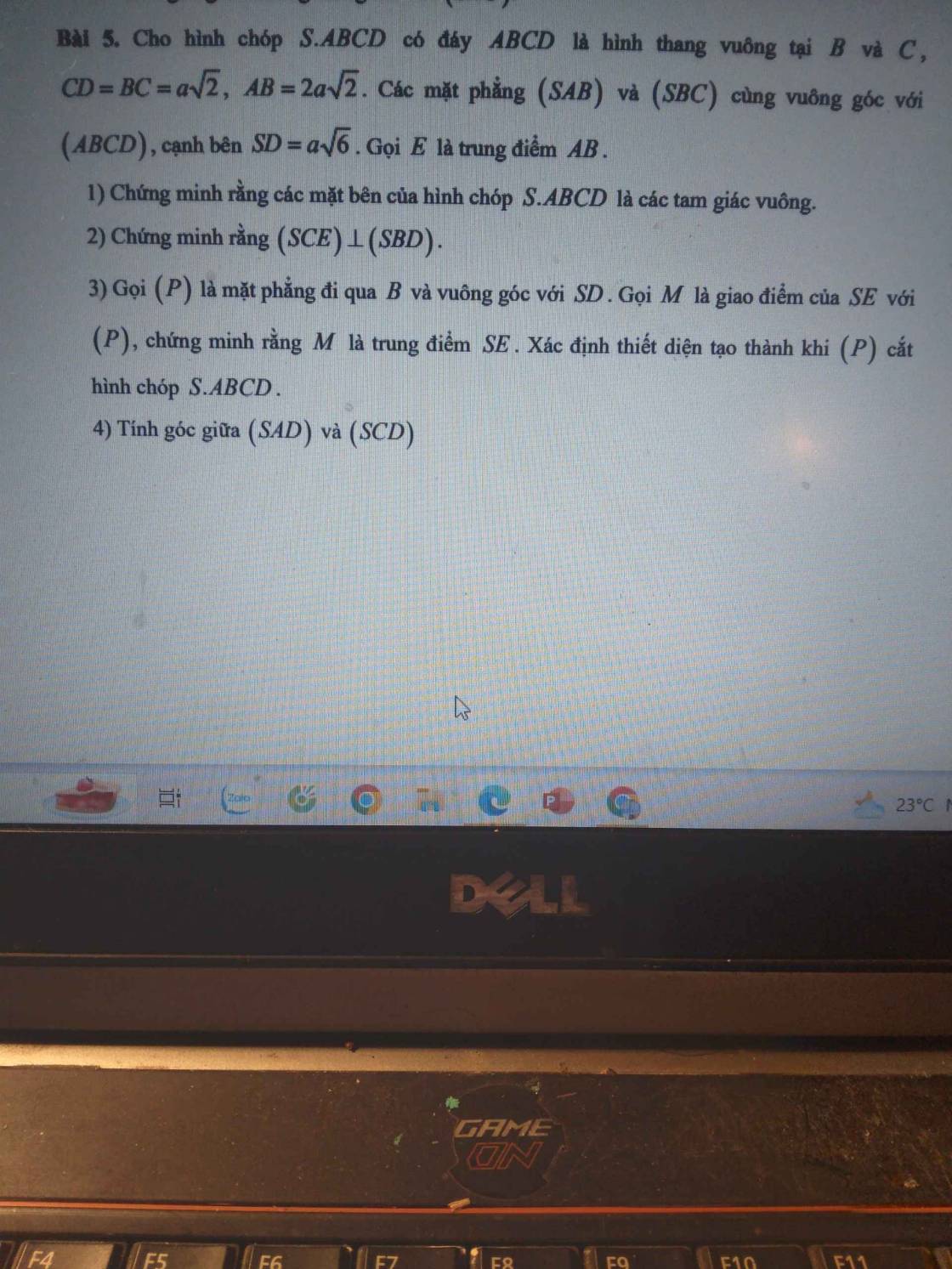giúp em câu 3 4 với ạ. Cần gấp
