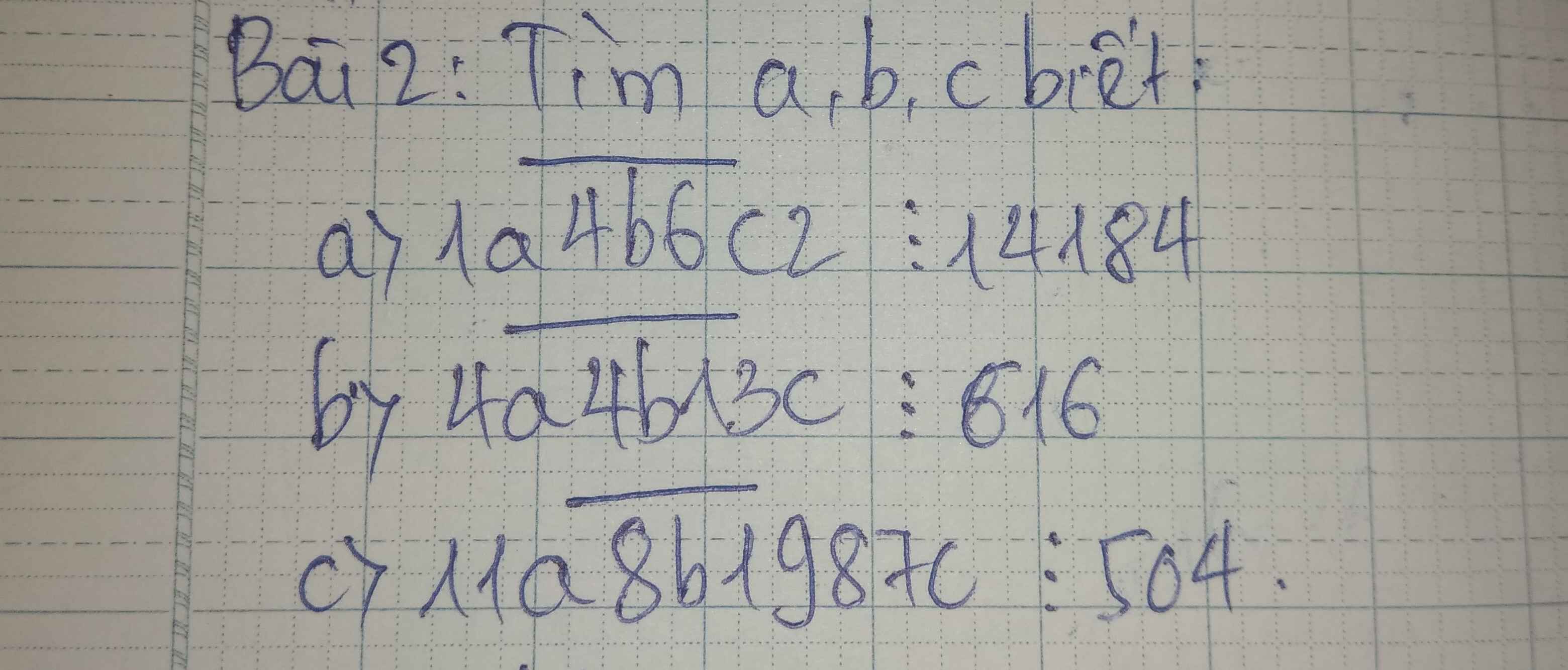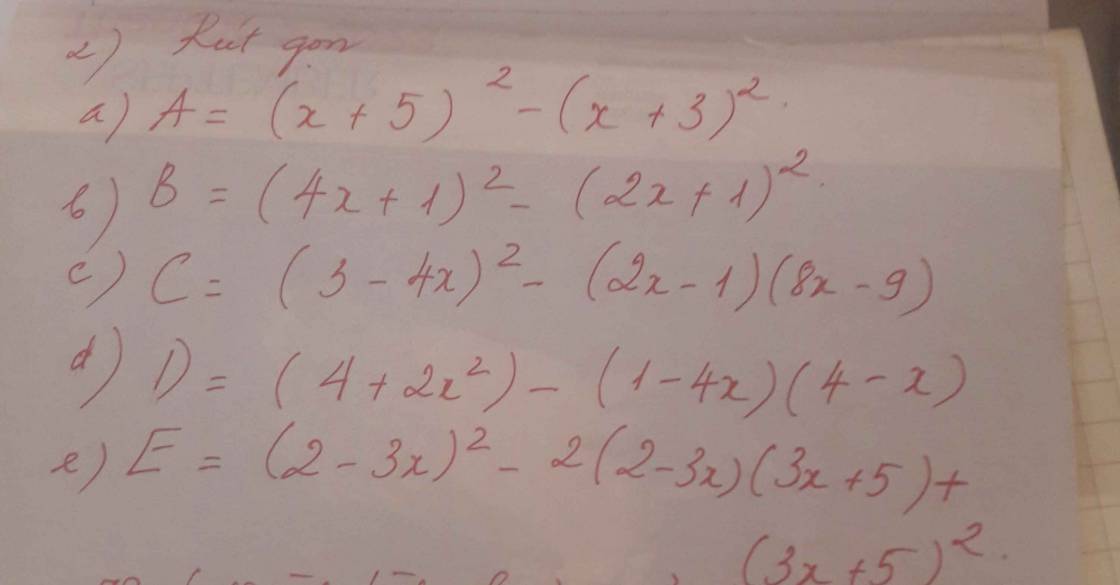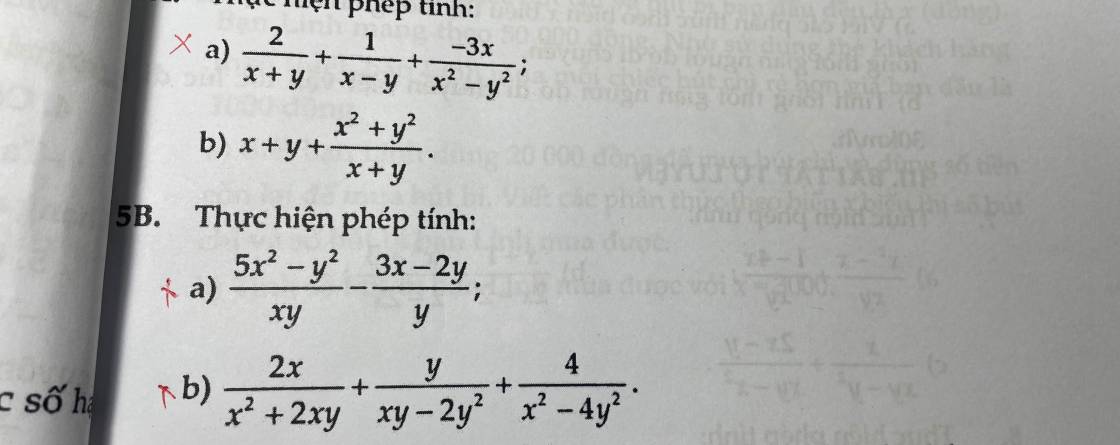Question

GIÚP ẠAA

Answer 1

Answer 2

a: Xét tứ giác AMHN có \(\hat{AMH}=\hat{ANH}=\hat{MAN}=90^0\)

nên AMHN là hình chữ nhật

b: Xét tứ giác AHPQ có

N là trung điểm chung của AP và HQ

=>AHPQ là hình bình hành

Hình bình hành AHPQ có AP⊥HQ

nên AHPQ là hình thoi

=>AP là phân giác của góc QAH

=>\(\hat{QAP}=\hat{HAP}\)

=>\(\hat{QAC}=\hat{HAC}\)

mà \(\hat{HAC}=\hat{ABC}\left(=90^0-\hat{HAB}\right)\)

nên \(\hat{QAC}=\hat{ABC}\)

c: IE⊥AB

CA⊥BA

Do đó: IE//AC

=>IK//AC

Xét ΔHAC có

I là trung điểm của HC

IK//AC

Do đó: K là trung điểm của HA