- Hàm số 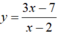 xác định trên R\ {2}.
xác định trên R\ {2}.
- Ta có:
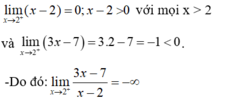
Chọn B.
- Hàm số 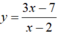 xác định trên R\ {2}.
xác định trên R\ {2}.
- Ta có:
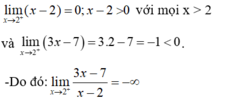
Chọn B.
Đạo hàm của hàm số \(y=\left(-x^2+3x+7\right)^7\) là:
A. \(y'=7\left(-2x+3\right)\left(-x^2+3x+7\right)^6\)
B. \(y'=7\left(-x^2+3x+7\right)^6\)
C. \(y'=\left(-2x+3\right)\left(-x^2+3x+7\right)^6\)
D. \(y'=7\left(-2x+3\right)\left(-x^2+3x+7\right)^6\)
Gọi `bb A` là giới hạn của hàm số `f(x)=[x+x^2+x^3+...+x^50 -50]/[x-1]` khi `x -> 1.` Tính giá trị của `bb A.`
Cho hàm số f ( x ) = x 2 - 5 k h i x ≥ 3 ( 1 ) x 2 - 5 x + 2 k h i x < 3 ( 2 )
Trong biểu thức (2) ở trên, cần thay số 5 bằng số nào để hàm số f(x) có giới hạn khi x → 3?
A. 19.
B. 1.
C. -1.
D. Không có số nào thỏa mãn.
Trong biểu thức (1) xác định hàm số y = f ( x ) ở Ví dụ 4, cần thay 2 bằng số nào để hàm số có giới hạn là -2 khi x → 1?
Giới hạn của hàm số f ( x ) = x 2 - ( a + 2 ) x + a + 1 x 3 - 1 khi x → 1 bằng:
A. - a 3
B. a 3
C. - a - 2 3
D. 2 - a 3
Biết hàm số y = f x = 3 x + b k h i x ≤ - 1 x + a k h i x > - 1 có giới hạn tại x= -1. Giá trị của a - b bằng
A. - 1
B. - 2
C. 2
D. 1
Tìm a để hàm số sau có giới hạn khi x → 2
f ( x ) = x 2 + a x + 2 khi x > 2 2 x 2 − x + 1 khi x ≤ 2
A. + ∞
B. − ∞
C. 1 2
D.1
Tính giới hạn của các hàm số sau khi x → +∞ và khi x → -∞ f x = x 2 - 3 x x + 2
Tìm a để hàm số sau có giới hạn khi lim x → 2 f ( x ) = x 2 + a x + 1 k h i x > 2 2 x 2 - x + 1 k h i x ≤ 2
A. +∞
B. -∞
C. 1/2
D. 1