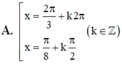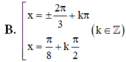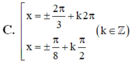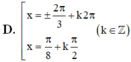Đặt \(t=\sin2x+cos2x\)
=>\(t^2=\left(\sin2x+cos2x\right)^2=1+2\cdot\sin2x\cdot cos2x\)
=>\(2\cdot\sin2x\cdot cos2x=t^2-1\)
=>\(\sin2x\cdot cos2x=\frac{t^2-1}{2}\)
Ta có: \(t=\sin2x+cos2x\)
=>\(t=\sqrt2\cdot\sin\left(2x+\frac{\pi}{4}\right)\)
Ta có: \(-1<=\sin\left(2x+\frac{\pi}{4}\right)\le1\)
=>\(-\sqrt2\le\sqrt2\cdot\sin\left(2x+\frac{\pi}{4}\right)\le\sqrt2\)
=>\(-\sqrt2\le t\le\sqrt2\)
Ta có: \(\left(\sin2x+cos2x\right)\left(1-\sin2x\cdot cos2x\right)+\sin2x\cdot cos2x=1\)
=>\(t\cdot\left(1-\frac{t^2-1}{2}\right)+\frac{t^2-1}{2}=1\)
=>\(t\cdot\frac{2-t^2+1}{2}+\frac{t^2-1}{2}=1\)
=>\(\frac{-t^3+3t+t^2-1}{2}=1\)
=>\(-t^3+t^2+3t-1=2\)
=>\(t^3-t^2-3t+1=-2\)
=>\(t^3-t^2-3t+3=0\)
=>\(\left(t-1\right)\left(t^2-3\right)=0\)
=>\(\left[\begin{array}{l}t-1=0\\ t^2-3=0\end{array}\right.\Rightarrow\left[\begin{array}{l}t=1\\ t^2=3\end{array}\right.\Rightarrow\left[\begin{array}{l}t=1\left(nhận\right)\\ t=\sqrt3\left(loại\right)\\ t=-\sqrt3\left(loại\right)\end{array}\right.\)
=>t=1
=>\(\sqrt2\cdot\sin\left(2x+\frac{\pi}{4}\right)=1\)
=>\(\sin\left(2x+\frac{\pi}{4}\right)=\frac{1}{\sqrt2}\)
=>\(\left[\begin{array}{l}2x+\frac{\pi}{4}=\frac{\pi}{4}+k2\pi\\ 2x+\frac{\pi}{4}=\pi-\frac{\pi}{4}+k2\pi=\frac34\pi+k2\pi\end{array}\right.\Rightarrow\left[\begin{array}{l}2x=k2\pi\\ 2x=\frac12\pi+k2\pi\end{array}\right.\)
=>\(\left[\begin{array}{l}x=k\pi\\ x=\frac{\pi}{4}+k\pi\end{array}\right.\)