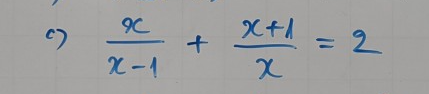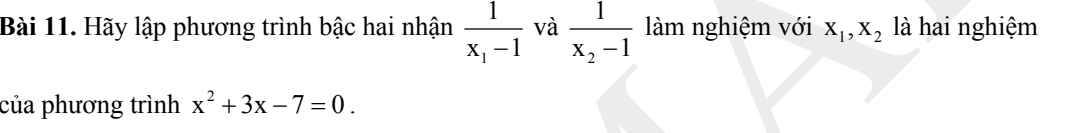ĐKXĐ: \(x\notin\left\{1;0\right\}\)
\(\dfrac{x}{x-1}+\dfrac{x+1}{x}=2\)
=>\(\dfrac{x^2+\left(x+1\right)\left(x-1\right)}{x\left(x-1\right)}=2\)
=>\(2x\left(x-1\right)=x^2+x^2-1=2x^2-1\)
=>-2x=-1
=>\(x=\dfrac{1}{2}\left(nhận\right)\)
\(\dfrac{x}{x-1}+\dfrac{x+1}{x}=2\left(x\ne1;x\ne0\right)\\ \Leftrightarrow\dfrac{x^2}{x\left(x-1\right)}+\dfrac{\left(x+1\right)\left(x-1\right)}{x\left(x-1\right)}=2\\ \Leftrightarrow\dfrac{x^2+x^2-1}{x\left(x-1\right)}=2\\ \Leftrightarrow2x^2-1=2x^2-2x\\ \Leftrightarrow2x=1\\ \Leftrightarrow x=\dfrac{1}{2}\left(tm\right)\)
\(\dfrac{x}{x-1}+\dfrac{x+1}{x}=2\) (ĐK:\(x\ne0;x\ne1\))
\(\Leftrightarrow\dfrac{x^2}{x\left(x-1\right)}+\dfrac{x^2-1}{x\left(x-1\right)}=2\)
\(\Leftrightarrow\dfrac{2x^2-1}{x^2-x}=2\)
\(\Leftrightarrow2x^2-2x=2x^2-1\)
\(\Leftrightarrow2x=1\)
\(\Leftrightarrow x=\dfrac{1}{2}\) (T/m)