c.
Qua E kẻ đường thẳng song song AB cắt BM tại D. Gọi F là trung điểm MD \(\Rightarrow F\in MB\)
\(\Rightarrow ED\perp MN\Rightarrow\Delta MED\) vuông tại E hay M, E, D cùng thuộc đường tròn đường kính MD
\(ED||AB\Rightarrow\widehat{MDE}=\widehat{MBA}\) (đồng vị)
\(\widehat{MBA}=\widehat{MCA}\) (cùng chắn AM)
\(\Rightarrow\widehat{MDE}=\widehat{MCA}\)
\(\Rightarrow MCDE\) nội tiếp
\(\Rightarrow M,C,E\) cùng thuộc đường tròn đường kính MD
Hay đường tròn ngoại tiếp tam giác CME có tâm F thuộc đường thẳng MB cố định
\(\Rightarrow\) Khoảng cách từ N đến tâm đường tròn ngoại tiếp CME là độ dài đoạn thẳng NF với F thuộc MB
\(\Rightarrow NF_{min}\) khi \(NF\perp MB\) hay F là hình chiếu vuông góc của N lên MB
Đặt \(OA=OB=R\Rightarrow AI=\dfrac{2}{3}R\) ; \(BI=2R-\dfrac{2}{3}R=\dfrac{4}{3}R\)
Hệ thức lượng trong tam giác vuông AMB:
\(MI^2=AI.BI=\dfrac{8}{9}R^2\Rightarrow MI=\dfrac{2R\sqrt{2}}{3}\) \(\Rightarrow MB=\sqrt{MI^2+IB^2}=\dfrac{2R\sqrt{6}}{3}\)
Hai tam giác vuông MNF và MBI đồng dạng (chung góc M)
\(\Rightarrow\dfrac{MF}{MI}=\dfrac{MN}{MB}\Rightarrow MF=\dfrac{MN.MI}{MB}=\dfrac{2MI^2}{MB}=\dfrac{4R\sqrt{6}}{9}=\dfrac{2}{3}MB\)
\(\Rightarrow MD=2MF=\dfrac{4}{3}MB\)
Áp dụng định lý Talet: \(\dfrac{MI}{ME}=\dfrac{MB}{MD}=\dfrac{3}{4}\Rightarrow MI=\dfrac{3}{4}ME\)
\(\Rightarrow ME=\dfrac{4}{3}MI\)
Hay C là điểm thuộc cung BC sao cho \(ME=\dfrac{4}{3}MI\)
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét tứ giác IECB có \(\widehat{ECB}+\widehat{EIB}=90^0+90^0=180^0\)
nên IECB là tứ giác nội tiếp
b: Xét ΔAIE vuông tại I và ΔACB vuông tại C có
\(\widehat{IAE}\) chung
Do đó; ΔAIE~ΔACB
=>\(\dfrac{AI}{AC}=\dfrac{AE}{AB}\)
=>\(AI\cdot AB=AC\cdot AE\)
\(AE\cdot AC-AI\cdot IB\)
\(=AI\cdot AB-AI\cdot IB\)
\(=AI\cdot\left(AB-IB\right)\)
\(=AI\cdot AI=AI^2\)
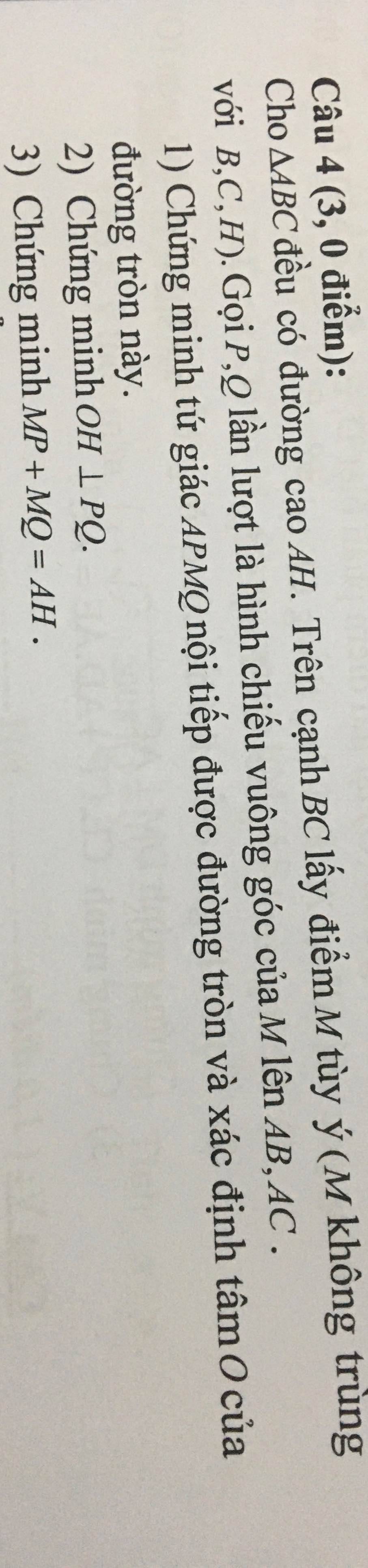
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
