a: \(\dfrac{1}{6}+\dfrac{1}{10}+...+\dfrac{2}{x\left(x+1\right)}=-\dfrac{11}{3}\)
=>\(2\left(\dfrac{1}{12}+\dfrac{1}{20}+...+\dfrac{1}{x\left(x+1\right)}\right)=-\dfrac{11}{3}\)
=>\(\dfrac{1}{12}+\dfrac{1}{20}+...+\dfrac{1}{x\left(x+1\right)}=-\dfrac{11}{6}\)
=>\(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{x}-\dfrac{1}{x+1}=-\dfrac{11}{6}\)
=>\(\dfrac{1}{3}-\dfrac{1}{x+1}=-\dfrac{11}{6}\)
=>\(\dfrac{1}{x+1}=\dfrac{1}{3}+\dfrac{11}{6}=\dfrac{13}{6}\)
=>\(x+1=\dfrac{6}{13}\)
=>\(x=-\dfrac{7}{13}\left(nhận\right)\)
b: Đặt \(A=1-5+5^2-5^3+...+\left(-5\right)^x\)
\(=\left(-5\right)^0+\left(-5\right)^1+...+\left(-5\right)^x\)
=>\(-5A=\left(-5\right)^1+\left(-5\right)^2+...+\left(-5\right)^{x+1}\)
=>\(-5A-A=\left(-5\right)^1+\left(-5\right)^2+...+\left(-5\right)^{x+1}-\left(-5\right)^0-\left(-5\right)^1-...-\left(-5\right)^x\)
=>\(-6A=\left(-5\right)^{x+1}-1\)
=>\(A=\dfrac{1-\left(-5\right)^{x+1}}{6}\)
Theo đề, ta có: \(A=\dfrac{25^{100}+1}{6}\)
=>\(\dfrac{1-\left(-5\right)^{x+1}}{6}=\dfrac{5^{200}+1}{6}\)
=>\(1-\left(-5\right)^{x+1}=5^{200}+1\)
=>\(-\left(-5\right)^{x+1}=5^{200}\)
=>\(\left(-5\right)^{x+1}=-5^{200}\)(1)
TH1: x+1 chẵn
=>x lẻ
Phương trình (1) sẽ tương ứng với \(5^{x+1}=-5^{200}\)
=>\(x+1=log_5\left(-5^{200}\right)\left(loại\right)\)
TH2: x+1 lẻ
=>x chẵn
(1) sẽ tương đương với \(5^{x+1}=5^{200}\)
=>x+1=200
=>x=199(loại)
Vậy: Không có giá trị nào của x thỏa mãn yêu cầu đề bài

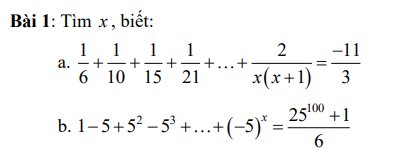







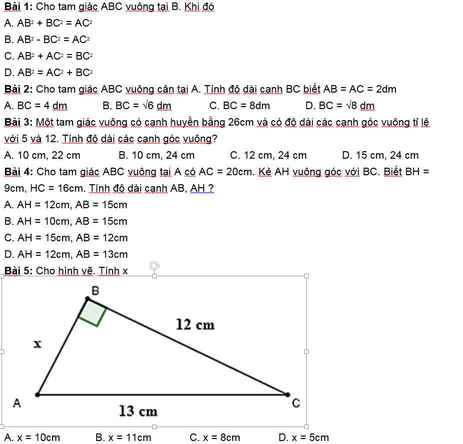



 Giải chi tiết hộ mình nha!!!
Giải chi tiết hộ mình nha!!!






