c: 12x-5y+6xy=28
=>\(12x+6xy-5y-10=18\)
=>\(6x\left(y+2\right)-5\left(y+2\right)=18\)
=>\(\left(6x-5\right)\left(y+2\right)=18\)
mà 6x-5 lẻ(do x nguyên)
nên \(\left(6x-5;y+2\right)\in\left\{\left(1;18\right);\left(-1;-18\right);\left(9;2\right);\left(-9;-2\right);\left(3;6\right);\left(-3;-6\right)\right\}\)
=>\(\left(6x;y\right)\in\left\{\left(6;16\right);\left(4;-20\right);\left(14;0\right);\left(-4;-4\right);\left(8;4\right);\left(2;-8\right)\right\}\)
mà 6x chia hết cho 6(do x là số nguyên)
nên \(\left(6x;y\right)=\left(6;16\right)\)
=>(x;y)=(1;16)
d: 2xy+2x-3y=-3
=>2x(y+1)-3y-3=-6
=>(2x-3)(y+1)=-6
mà 2x-3 lẻ
nên \(\left(2x-3;y+1\right)\in\left\{\left(1;-6\right);\left(-1;6\right);\left(3;-2\right);\left(-3;2\right)\right\}\)
=>\(\left(2x;y\right)\in\left\{\left(4;-7\right);\left(2;5\right);\left(6;-3\right);\left(0;1\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(2;-7\right);\left(1;5\right);\left(3;-3\right);\left(0;1\right)\right\}\)
a: 6x+y+2xy=3
=>\(6x+2xy+y-3=0\)
=>\(2x\left(y+3\right)+y+3-6=0\)
=>\(\left(2x+1\right)\left(y+3\right)=6\)
mà 2x+1 lẻ
nên \(\left(2x+1;y+3\right)\in\left\{\left(1;6\right);\left(-1;-6\right);\left(3;2\right);\left(-3;-2\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(0;3\right);\left(-1;-9\right);\left(1;-1\right);\left(-2;-5\right)\right\}\)
b: 4x+3y+4xy=9
=>\(4x\left(y+1\right)+3y+3=12\)
=>(y+1)(4x+3)=12
=>(4x+3)(y+1)=12
mà 4x+3 lẻ
nên \(\left(4x+3;y+1\right)\in\left\{\left(1;12\right);\left(-1;-12\right);\left(3;4\right);\left(-3;-4\right)\right\}\)
=>\(\left(4x;y\right)\in\left\{\left(-2;11\right);\left(-4;-13\right);\left(0;3\right);\left(-6;-5\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(-\dfrac{1}{2};11\right);\left(-1;-13\right);\left(0;3\right);\left(-\dfrac{3}{2};-5\right)\right\}\)
mà x,y nguyên
nên \(\left(x;y\right)\in\left\{\left(-1;-13\right);\left(0;3\right)\right\}\)

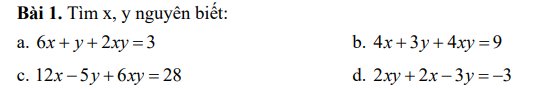




 Giúp mình với aa (Giải chi tiết + nếu được thì thêm lời giải thích ở cuối bài làm giúp mình nha
Giúp mình với aa (Giải chi tiết + nếu được thì thêm lời giải thích ở cuối bài làm giúp mình nha