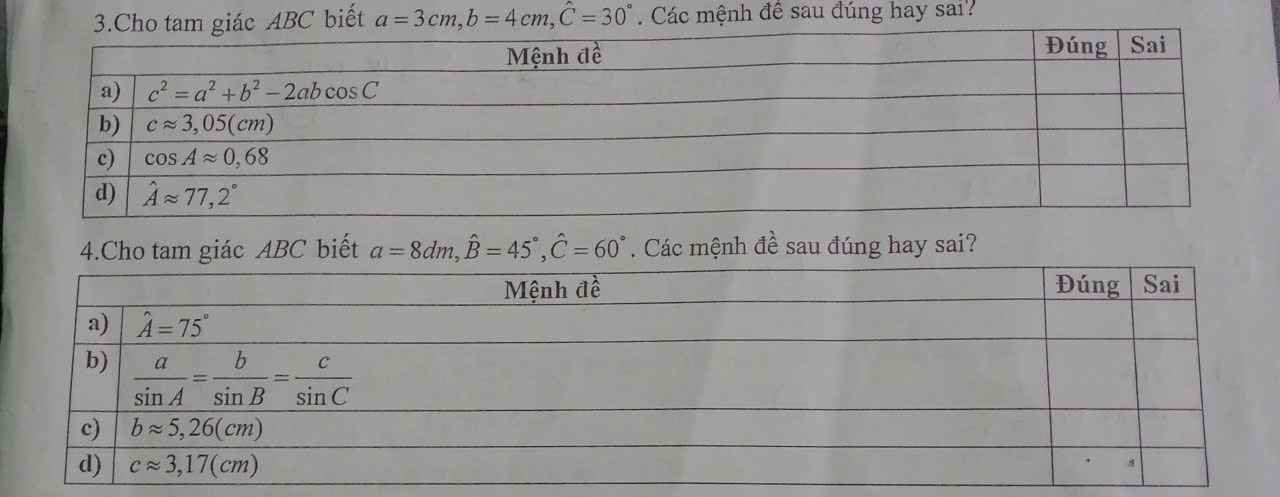3:
a: Xét ΔABC có \(cosC=\dfrac{CA^2+CB^2-AB^2}{2\cdot CA\cdot CB}\)
=>\(\dfrac{b^2+a^2-c^2}{2ba}=cosC\)
=>\(a^2+b^2-c^2=2ab\cdot cosC\)
=>\(c^2=a^2+b^2-2ab\cdot cosC\)
=>Đúng
b: \(c^2=a^2+b^2-2ba\cdot cosC=3^2+4^2-2\cdot3\cdot4\cdot cos30=25-12\sqrt{3}\)
=>\(c=\sqrt{25-12\sqrt{3}}\simeq2,05\left(cm\right)\)
=>Sai
c: \(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{b^2+c^2-a^2}{2bc}\)
\(=\dfrac{4^2+25-12\sqrt{3}-3^2}{2\cdot4\cdot\sqrt{25-12\sqrt{3}}}\)
=>\(cosA\simeq0,68\)
=>Đúng
d: Sai
4:
a: Xét ΔABC có \(\widehat{B}+\widehat{C}+\widehat{A}=180^0\)
=>\(\widehat{A}=180^0-45^0-60^0=75^0\)
=>Đúng
b: Đúng
c: \(\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}\)
=>\(\dfrac{8}{sin75}=\dfrac{b}{sin45}=\dfrac{c}{sin60}\)
=>\(\left\{{}\begin{matrix}b=8\cdot\dfrac{sin45}{sin75}\simeq5,86\left(dm\right)=58,6\left(cm\right)\\c=8\cdot\dfrac{sin60}{sin75}\simeq7,17\left(dm\right)=71,7\left(cm\right)\end{matrix}\right.\)
=>Sai
d: Sai
giải chi tiết giúp mình với ạ 
