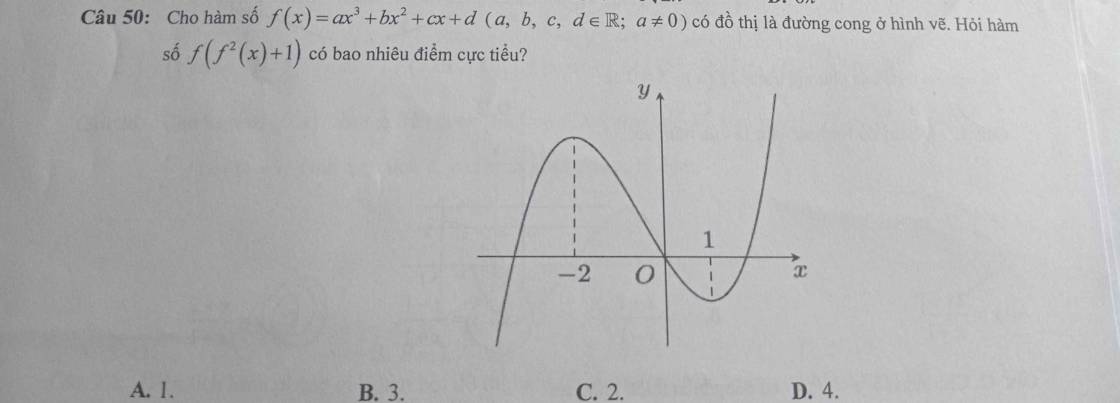
Căn cứ vào dạng đồ thị ($a>0$), ta thấy đây là hàm bậc 3 và có đạo hàm là \(f'\left(x\right)=3a\left(x+2\right)\left(x-1\right)\) (*).

\(\left(f\left(f^2\left(x\right)+1\right)\right)'=f'\left(f^2\left(x\right)+1\right).2f\left(x\right).f'\left(x\right)=0\)
\(\Leftrightarrow\)\(\left[{}\begin{matrix}f'\left(f^2\left(x\right)+1\right)=0\left(1\right)\\f\left(x\right)=0\left(2\right)\\f'\left(x\right)=0\left(3\right)\end{matrix}\right.\)
Khảo sát (*), ta thấy khi $x \geq 1$ thì \(f'\left(x\right)\ge0\) , do đó với phương trình $(1)$, $f^2(x)+1 \geq 1$ nên $f'(f^2(x)+1) \geq 0$, dấu bằng xảy ra khi $f^2(x)+1=1$, tương đương với $f^2(x)=0$. Điều này ta không cần quan tâm đến, do nghiệm của phương trình này đều là nghiệm kép, và quan trọng hơn $f'(f^2(x)+1)$ mang dấu dương với mọi $x$.
Ở phương trình số (2), từ đồ thị đề bài cho ta thấy có 2 nghiệm mà giá trị của hàm số đi từ âm sang dương, do đó ta tìm được hai điểm cực tiểu.
Ở phương trình số (3), từ đồ thị của hàm $f(x)=(x+2)(x-1)$ , ta thấy $x=1$ giá trị của hàm số này đi từ âm sang dương, do đó ta tìm thêm được một điểm cực tiểu.
Vậy, hàm số đề cho có 3 điểm cực tiểu.