Xét ΔOAB có \(OA^2+OB^2=AB^2\)
nên ΔOAB vuông cân tại O
=>\(\widehat{AOB}=90^0\)
Độ dài cung nhỏ AB là:
\(\dfrac{\Omega\cdot R\cdot90}{180}=\Omega\cdot\dfrac{R}{2}\)
=>Chọn A
Đúng 0
Bình luận (0)
\(OA=OB=R\Rightarrow OA^2+OB^2=2R^2=\left(R\sqrt{2}\right)^2=AB^2\)
\(\Rightarrow\Delta OAB\) vuông tại O \(\Rightarrow\widehat{AOB}=90^0\)
\(\Rightarrow l_{\stackrel\frown{AB}}=\dfrac{90}{360}.2\pi R=\dfrac{\pi R}{2}\)
Đúng 0
Bình luận (0)

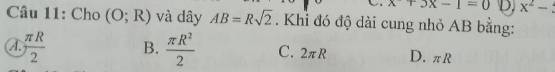





 giải giúp em ý nào cũng được ạ, giải chi tiết ạ
giải giúp em ý nào cũng được ạ, giải chi tiết ạ