i: \(\Leftrightarrow x\left(x+2\right)-2=x-2\)
=>x^2+2x=x
=>x^2+x=0
=>x(x+1)=0
=>x=0(loại) hoặc x=-1(nhận)
j: \(\Leftrightarrow\dfrac{-5}{\left(x-2\right)\left(x-3\right)}-\dfrac{x+3}{x-2}=0\)
=>-5-(x+3)(x-3)=0
=>x^2-9+5=0
=>x^2-4=0
=>x=2(loại) hoặc x=-2(nhận)
k: \(\Leftrightarrow\dfrac{x}{2\left(x+1\right)}-\dfrac{2x}{\left(x-3\right)\left(x+1\right)}=\dfrac{-x}{2\left(x-3\right)}\)
=>x(x-3)-4x=-x(x+1)
=>x^2-3x-4x+x^2+x=0
=>2x^2-6x=0
=>2x(x-3)=0
=>x=3(loại) hoặc x=0(nhận)
l: \(\Leftrightarrow x^2+x+1-3x^2=2x\left(x-1\right)\)
=>2x^2-2x=-2x^2+x+1
=>4x^2-3x-1=0
=>4x^2-4x+x-1=0
=>(x-1)(4x+1)=0
=>x=1(loại) hoặc x=-1/4(nhận)
m: \(\Leftrightarrow\dfrac{x+25}{2\left(x-5\right)\left(x+5\right)}-\dfrac{x+5}{x\left(x-5\right)}=\dfrac{-\left(x-5\right)}{2x\left(x+5\right)}\)
\(\Leftrightarrow x\left(x+25\right)-2\left(x+5\right)^2=-\left(x-5\right)^2\)
=>\(x^2+25x-2x^2-20x-50=-x^2+10x-25\)
=>5x-50=10x-25
=>-5x=25
=>x=-5(loại)

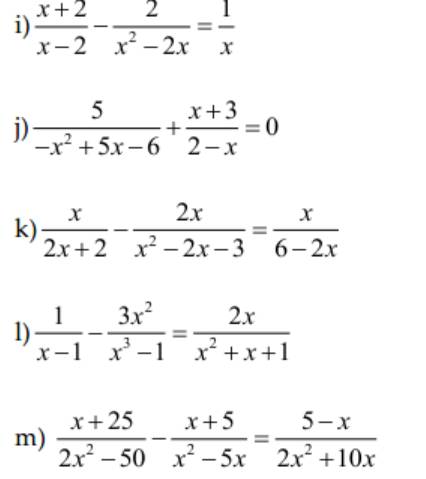








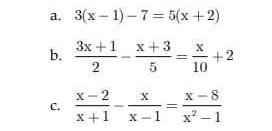

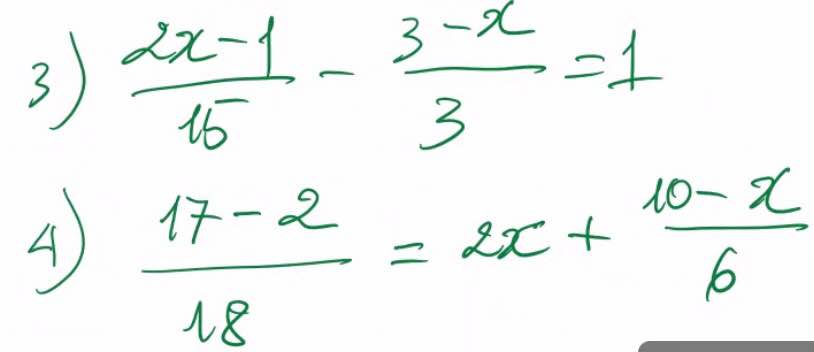

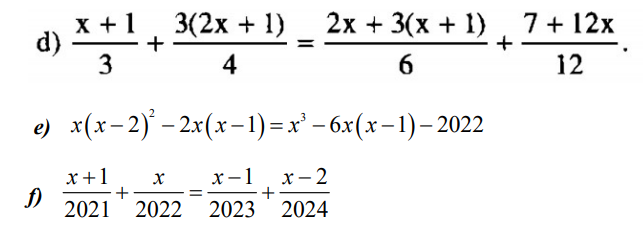
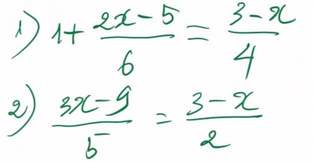

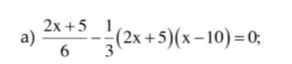


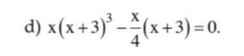

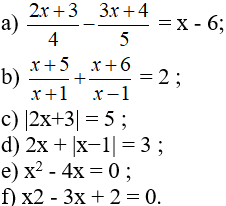

 giải các phương trình sau
giải các phương trình sau