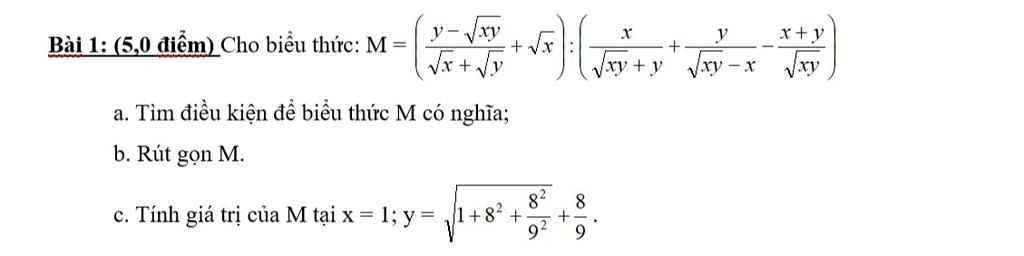a)
ĐK: \(x\ge0,y\ge0,\) x và y không đồng thời bằng 0
b)
\(M=\left(\dfrac{y-\sqrt{xy}}{\sqrt{x}+\sqrt{y}}+\sqrt{x}\right):\left(\dfrac{x}{\sqrt{xy}+y}+\dfrac{y}{\sqrt{xy}-x}-\dfrac{x+y}{\sqrt{xy}}\right)\)
\(M=\left(\dfrac{\left(y-\sqrt{xy}\right)\left(\sqrt{x}-\sqrt{y}\right)}{x-y}+\dfrac{\sqrt{x}\left(x-y\right)}{x-y}\right):\left(\dfrac{x\left(\sqrt{xy}-x\right)+y\left(\sqrt{xy}+y\right)}{\left(\sqrt{xy}+y\right)\left(\sqrt{xy}-x\right)}-\dfrac{x+y}{\sqrt{xy}}\right)\)
\(M=\left(\dfrac{2y\sqrt{x}-\sqrt{y^3}-x\sqrt{y}}{x-y}+\dfrac{\sqrt{x^3}-y\sqrt{x}}{x-y}\right):\left(\dfrac{x\sqrt{xy}-x^2+y\sqrt{xy}+y^2}{\sqrt{xy}\left(y-x\right)}+\dfrac{\left(x+y\right)\left(x-y\right)}{\sqrt{xy}\left(y-x\right)}\right)\)
\(M=\dfrac{\sqrt{x^3}-\sqrt{y^3}+y\sqrt{x}-x\sqrt{y}}{x-y}:\dfrac{x\sqrt{xy}+y\sqrt{xy}-x^2+y^2+x^2-y^2}{\sqrt{xy}\left(y-x\right)}\)
\(M=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)-\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}{x-y}:\dfrac{\sqrt{xy}\left(x+y\right)}{\sqrt{xy}\left(y-x\right)}\)
\(M=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(x+y\right)}{x-y}:\dfrac{x+y}{y-x}\)
\(M=\dfrac{\left(x+y\right)\left(\sqrt{x}-\sqrt{y}\right)}{x-y}\cdot\dfrac{-\left(x-y\right)}{x+y}\)
\(M=-\sqrt{x}+\sqrt{y}\)
c)
Ta có: \(y=\sqrt{1+8^2+\dfrac{8^2}{9^2}}+\dfrac{8}{9}=\sqrt{1+64+\dfrac{64}{81}}+\dfrac{8}{9}=\dfrac{73}{9}+\dfrac{8}{9}=\dfrac{81}{9}=9\)
Thay x=1, y=9 TMĐK vào M ta có:
\(M=-\sqrt{1}+\sqrt{9}=-1+3=2\)