a, Pt hoành độ giao điểm
\(\dfrac{1}{2}x^2+3x+3m-\dfrac{1}{2}m^2=0\Leftrightarrow x^2+6x+6m-m^2=0\)
\(\Delta'=9-\left(-m^2+6m\right)=\left(m-3\right)^2\)
Để (P) tiếp xúc (d) khi m = 3
Thay m = 3 vào pt ta được \(x^2+6x+9=0\Leftrightarrow x=-3\Rightarrow y=-\dfrac{1}{2}.9=-\dfrac{9}{2}\)
Vậy (P) tiếp xúc (d) tại A(-3;-9/2)
b, Ta có \(\Delta=\left(m-3\right)^2\)>=0
Vậy pt luôn có 2 nghiệm x1;x2
\(\Rightarrow x_1=-3-\left(m-3\right)=-m;x_2=-3+\left(m-3\right)=-6+m\)
\(\Rightarrow-m^3+m=-8m-\dfrac{\left(m-6\right)^2-m^2}{6}\)
\(\Leftrightarrow-6m^3+6m=-48m-\left(-12m+36\right)\)
\(\Leftrightarrow6m^3-42m-36=0\Leftrightarrow m=3;-1;2\)

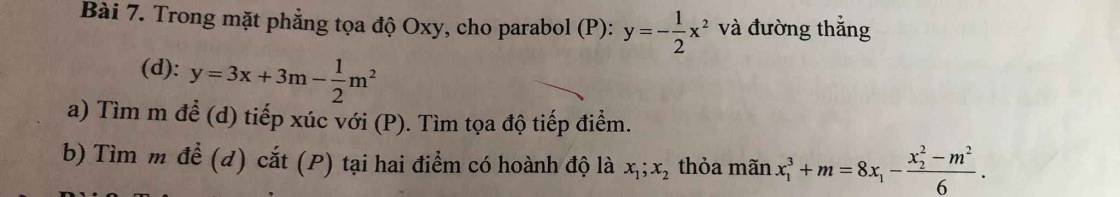



 cíu tui cíu tui
cíu tui cíu tui cíu tui cíu tui
cíu tui cíu tui

 cíu tui cíu tui
cíu tui cíu tui

 cíu cíu
cíu cíu cíu lẹ cíu lẹ
cíu lẹ cíu lẹ