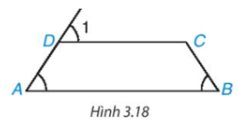
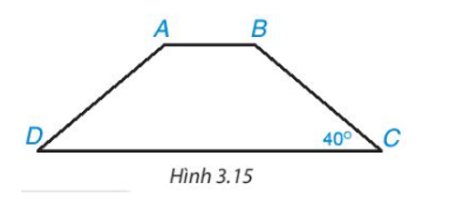
a: Xét ΔADB có
Q,M lần lượt là trung điểm của AD,AB
=>QM là đường trung bình của ΔADB
=>QM//BD và \(QM=\dfrac{BD}{2}\left(1\right)\)
Xét ΔCBD có
P,N lần lượt là trung điểm của CD,CB
=>PN là đường trung bình của ΔCBD
=>PN//BD và \(PN=\dfrac{BD}{2}\left(2\right)\)
Từ (1),(2) suy ra QM//PN và QM=PN
=>MNPQ là hình bình hành
Xét ΔCAB có
I,N lần lượt là trung điểm của CA,CB
=>IN là đường trung bình của ΔCAB
=>IN//AB và \(IN=\dfrac{AB}{2}\left(3\right)\)
Xét ΔDAB có
Q,K lần lượt là trung điểm của DA,DB
=>QK là đường trung bình của ΔDAB
=>QK//AB và \(QK=\dfrac{AB}{2}\left(4\right)\)
Từ (3),(4) suy ra IN//QK và IN=QK
=>INKQ là hình bình hành
b: ta có: INKQ là hình bình hành
=>IK cắt NQ tại trung điểm của mỗi đường(1)
Ta có: MNPQ là hình bình hành
=>MP cắt NQ tại trung điểm của mỗi đường(2)
Từ (1),(2) suy ra IK,MP,NQ đồng quy