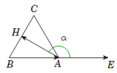
Vẽ A E → = B A → .
Khi đó A H → , A E → = H A E ^ = α (hình vẽ)
= 180 0 − B A H ^ = 180 0 − 30 0 = 150 0 .
Chọn D.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho tam giác ABC, biết góc A bằng 600, AC = 8cm, AB = 5cm. Tính độ dài đường cao AH?
A. 4,56
B. 4,95
C. 5,42
D. Đáp án khác
Cho tam giác Abc có A(1;2) B(5;0) C(0;1). Viết ptts của a. AB, BC, CA b. Trung tuyến AM c. Đường cao AH d. Đường trung trực của AB
Cho tam giác ABC, biết A (4,3), B(-1,-1), C (2,-4)
a. Tìm tọa độ trực tâm H của tam giác ABC
b. Tìm điểm K là chân đường cao kẻ từ C
c. Tính chu vi tam giác ABC
d. Tính số đo góc A, B, C trong tam giác ABC
e. Tìm điểm N thuộc Oy sao cho N cách đều A và B
Cho các mệnh đề :A : “Nếu tam giác ABC đều có cạnh bằng a, đường cao là h thì
h
a
3
2
”B : “Tứ giác có bốn cạnh bằng nhau là hình vuông”C : “15 là số nguyên tố” D : “
225
là một số nguyên”Chọn câu sai: A. Mệnh đề A B sai B. Mệnh đề A
⇔
D đúng C. Mệnh đề B
⇔
C đúng D. Mệnh đề D sai
Đọc tiếp
Cho các mệnh đề :
A : “Nếu tam giác ABC đều có cạnh bằng a, đường cao là h thì h = a 3 2 ”
B : “Tứ giác có bốn cạnh bằng nhau là hình vuông”
C : “15 là số nguyên tố”
D : “ 225 là một số nguyên”
Chọn câu sai:
A. Mệnh đề A => B sai
B. Mệnh đề A ⇔ D đúng
C. Mệnh đề B ⇔ C đúng
D. Mệnh đề => D sai
Tam giác ABC vuông tại A có đường cao AH h và có BC a, CA b, AB c. Gọi BH c’ và CH b’(h.2.11). Hãy điền vào các ô trống trong các hệ thức sau đây để được các hệ thức lượng trong tam giác vuông:a2 b2 + (.....)b2 a x (.....)c2 a x (.....)h2 b’ x (.....)ah b x (.....)
Đọc tiếp
Tam giác ABC vuông tại A có đường cao AH = h và có BC = a, CA = b, AB = c. Gọi BH = c’ và CH = b’(h.2.11). Hãy điền vào các ô trống trong các hệ thức sau đây để được các hệ thức lượng trong tam giác vuông:
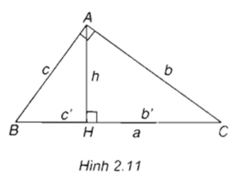
a2 = b2 + (.....)
b2 = a x (.....)
c2 = a x (.....)
h2 = b’ x (.....)
ah = b x (.....)
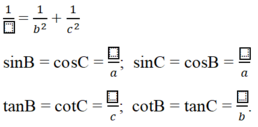
Cho tam giác ABC có A(1,2), B(3,5), C(-2,4). Độ dài đường cao AH của tam giác là?
trên trục oxy cho tam giác abc với a(1;2) , b( 2;3) ;c(4;6).a) viết phương trình đường cao ah.b) tính độ cao ah
Cho tam giác ABC có \(A=60^0\), cạnh \(CA=8cm\), cạnh \(AB=5cm\)
a. Tính BC
b. Tính diện tích tam giác ABC
c. Tính độ dài đường cao AH
d. Tính R
Cho tam giác đều ABC cạnh a, đường cao AH, trọng tâm G. Tính:
a, |AC|, |AB + AH|, |AB - AH|
b, |GB|, |GA + GB|, |GA + GB + GC|
Trong mặt phẳng Oxy cho tam giác ABC. A ( 1;2 ) B ( 2;0) C(-1;0)
a ) Viết phương trình tham số AB
b) Viết phương trình tổng quát đường thẳng BC
c) viết phương trình tổng quát đường cao AH và tìm tọa độ điểm H
d) tính góc hợp bởi ( AH , AB)
e) tính khoảng cách từ A đến BC