Xét `\Delta MHF` và `\Delta MKE`:
`\text {MH = MK (gt)}`
$\widehat {KME} = \widehat {HMF} (\text {đối đỉnh})$
`\text {ME = MF (trung tuyến DM)}`
`=> \Delta MHF = \Delta MKE (c-g-c).`
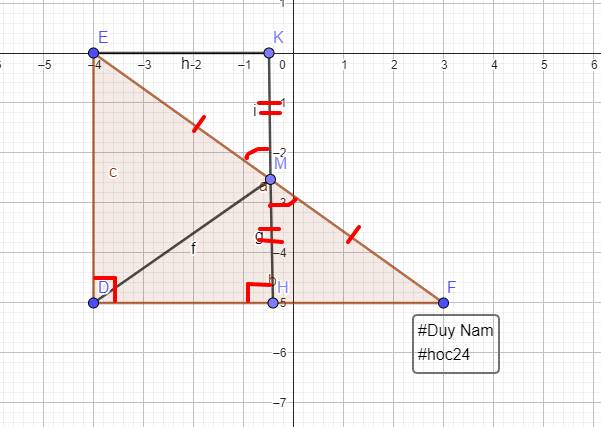
Xét ΔMHF và ΔMKE có
MH=MK
góc HMF=góc KME
MF=ME
=>ΔMHF=ΔMKE
Xét `\Delta MHF` và `\Delta MKE`:
`\text {MH = MK (gt)}`
$\widehat {KME} = \widehat {HMF} (\text {đối đỉnh})$
`\text {ME = MF (trung tuyến DM)}`
`=> \Delta MHF = \Delta MKE (c-g-c).`

Xét ΔMHF và ΔMKE có
MH=MK
góc HMF=góc KME
MF=ME
=>ΔMHF=ΔMKE
Cho tam giác DEF vuông tại d ,đường phân giác của góc E cắt DF tại M. Vẽ MH vuông góc với EF
a) Chứng minh tam giác DEM = tam giác HEM
b)Chứng minh MD=MH
c) Trên tia đối của tia DE lấy K sao cho DK = HF. Chứng minh 3 điểm K , M, H thẳng hàng.
Cho tam giác DEF vuông ở E. Tia phân giác của góc D ( M thuộc EF ). Từ M vẽ MH vuông góc với DF ( H thuộc DF )
a, Chứng minh: tam giác DEM = tam giác DHM
b, Gọi K là giao điểm của tia DE và tia MH. Tam giác KMF là tam giác gì? Vì sao?
c, C/m: KM+ME<KF
Cho tam giác ABC vuông tại A. Vẽ trung tuyến AM (AM thuộc BC). Từ M kẻ MH vuông góc AC. Trên tia đối của MH lấy điểm K sao cho MK = MH a) Chứng minh tam giác MHC = tam giác MKB b) Chứng minh AB vuông góc AC c) Gọi G là trung điểm của BH và AM, I là trung điểm của AB. Chứng minh I, G, C thẳng hàng
Cho tam giác DEF có DE DF tia phân giác của góc EDF cắt EF tại điểm MA Chứng minh tam giác DEM bằng tam giác FDMB vẽ MH vuông góc với DE tại H, DK vuông góc với DF tại K Chứng minh tam giác DMH bằng tam giác DMK
cho tam giác DEF vuông tại D . Có DE =6cm , EF=10cm
a) tính độ dài DF
b)vẽ tia phân giác ÊM của góc DEF (M thuộc DF). Từ M vẽ MH vuông góc với EF tại H . Chứng minh tam giác DEM= tam giác HEM
c) trên tia ED lấy K sao cho EF=EK
chứng minh: K,M,H thẳng hàng
Cho tam giác ABC vuông tại A, vẽ trung tuyến AM(M thuộc BC). Tù M kẻ MH vuông góc AC, Trên tia đối MH lấy điểm K sao cho MK bằng MH.
a) Chứng minh: Tan giac MHC=Tam giác MKB
b)Chứng minh: Tam giác ABH=Tam giác KHB
c)Gọi G là giao điểm của BH và AM, I là trung điểm của AB. Chứng minh I,G,C thẳng hàng
Cho tam giác DEF vuông tại D . Có DE = 6 cm , EF = 10 cm .
a ) Tính độ dài DF
b ) Vẽ tia phân giác EM của DEF ( M e DF ) . Từ M vẽ MH vuông góc với EF tại H . Chứng minh rằng Tam giác DEM = Tam giác HEM
c ) Trên tia ED lấy K sao cho EK = EF
Chứng minh rằng : ba điểm K , M , H thẳng hàng
bác nào vào giải giúp em :))
Cho tam giác ABC vuông tại A, vẽ trung tuyến AM( M thuộc BC). Từ M kẻ MH vuông góc với AC, trên tia đối của tia MH lấy điểm K sao cho MK = MH.
a, Chứng minh tam giác MHC = tam giác MKB
b, Chứng minh AB song song với MH
c, Gọi G là giao điểm của BH và AM, I là trung điểm của AB. Chứng minh I,G,C thẳng hàng.