Ôn thi vào 10
Các câu hỏi tương tự
Cho tam giác ABC vuông tại A AB lớn hơn AC đường cao AH Gọi E F lần lượt là hình chiếu của H trên AB AC a. Chứng minh AE x AB = AF x AC b. Vẽ đường tròn tâm O đường kính BC Chứng minh A thuộc đường tròn tâm O c. Gọi M là trung điểm của AC tiếp tuyến của O tại A cắt tia OM tại N Chứng minh NC là tiếp tuyến của đường tròn tâm O tại C
Cho ∆ABC nhọn có AB < AC. Vẽ đường tròn tâm O đường kính BC cắt các cạnh AB, AC lần lượt tại E và D . Gọi H là giao điểm BD và CE; AH cắt BC tại I.
a) Chứng minh AI vuông góc với BC
b) Vẽ AM, AN tiếp xúc (O) tại M và N. Chứng minh IA là tia phân giác góc \(\widehat{MIN}\)
c) Chứng minh ba điểm M, H , N thẳng hàng.
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết BH=8 cm,CH=18 cm.Gọi D,E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC . Gọi M và N lần lượt là trung điểm của HB và HC . Tính SDENM ?
2 Cho tam giác ABC vuông tại A, đường cao AH. Biết AC = 4cm BC = 5cm m) Tinh BH.AH hat B' (độ lớn của góc làm tròn kết quả đến phút) b) Gọi E và F lần lượt là hình chiếu của H trên AB, AC. Chứng minh . AE.AB = AF.AC c) Gọi M là trung điểm của BC. Chứng minh S AEMF = 1/ 2 S ABC
Bài 1: Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Kẻ đường cao AH
a) Giải tam giác vuông ABC (góc làm tròn đến phút).
b) Gọi G, K là hình chiếu của H lần lượt lên AB và AC. Chứng minh rằng: AG.AB=AK.AC
Bài 2: Cho vuông tại A, đường cao AH có , đường cao AH có HB=9cm,HC=16cm
a) Tính AB, AC và AH.
b) Hạ HD vuông góc AB,HE vuông góc AC . Tính chu vi và diện tích tứ giác ADHE.
Cho tam giác ABC vuông tại A (AB > AC).Đường cao AH , trung tuyến AM,phân giác AD lần lượt cắt đường tròn ngoại tiếp tam giác tại S,N,P.
a.Chứng minh MP // AH.
b.So sánh góc MAP,MPA và PAS.
c.Chứng minh AD là tia phân giác của góc MAH.
Cho tam giác ABC có cạnh AB AC. Các đường cao AD và BE của tam giác ABC cắt nhau tại H. Gọi I đối xứng với H qua D. Gọi M và N lần lượt là hình chiếu vuông góc của I trên AB và AC.a) Chứng minh tứ giác ABDE nội tiếp và góc widehat{CAD}widehat{CBI} ?b) Chứng minh rằng góc widehat{MDI}widehat{ACI} và tam giác ACI đồng dạng với tam giác MDI ?c) Gọi P và Q lần lượt là trung điểm của MD và AC. Chứng minh rằng góc widehat{IPQ}90^0 ?P/s: Nhờ thầy cô và các bạn giúp đỡ ý c với ạ, cám ơn n...
Đọc tiếp
Cho tam giác ABC có cạnh AB < AC. Các đường cao AD và BE của tam giác ABC cắt nhau tại H. Gọi I đối xứng với H qua D. Gọi M và N lần lượt là hình chiếu vuông góc của I trên AB và AC.
a) Chứng minh tứ giác ABDE nội tiếp và góc \(\widehat{CAD}=\widehat{CBI}\) ?
b) Chứng minh rằng góc \(\widehat{MDI}=\widehat{ACI}\) và tam giác ACI đồng dạng với tam giác MDI ?
c) Gọi P và Q lần lượt là trung điểm của MD và AC. Chứng minh rằng góc \(\widehat{IPQ}=90^0\) ?
P/s: Nhờ thầy cô và các bạn giúp đỡ ý c với ạ, cám ơn nhiều ạ!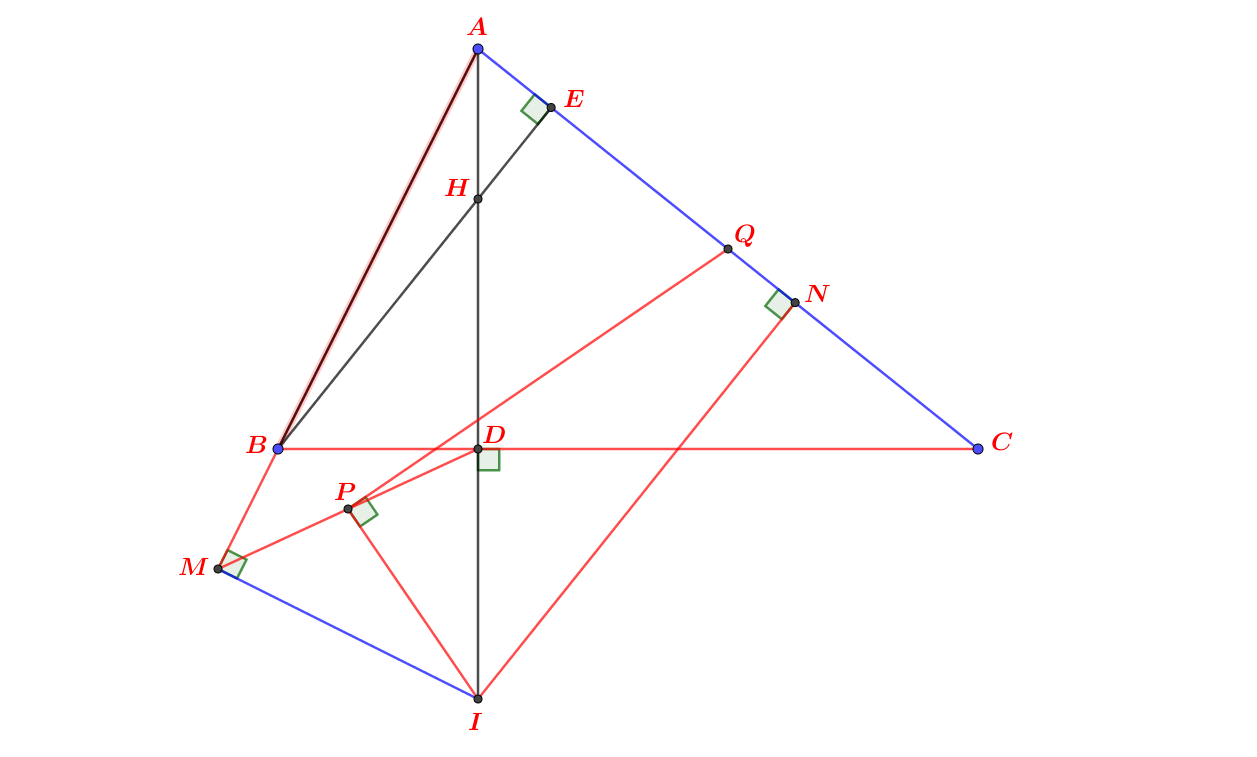
Cho tam giác ABC vuông tại A (AB > AC).Đường cao AH , trung tuyến AM,phân giác AD lần lượt cắt đường tròn ngoại tiếp tam giác tại S,N,P.
a.Chứng minh MP // AH.
b.So sánh góc MAP,MPA và PAS.
Cho tam giác ABC vuông tại A (AB > AC).Đường cao AH , trung tuyến AM,phân giác AD lần lượt cắt đường tròn ngoại tiếp tam giác tại S,N,P.
a.Chứng minh MP // AH.
b.So sánh góc MAP,MPA và PAS.








