Question

Cho tam giác ABC vuông tại A, AB = 6cm AC=8cm. Vẽ đường cao AH, đường phân giác BD. a) Tính AD, DC? b) Gọi I là giao điểm của AH và BD. Chứng minh rằng AB.BI=BD.HB c) Chứng minh rằng : tam giác AID cân.

Answer 1

a: Ta có: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC^2=6^2+8^2=100=10^2\)

=>BC=10(cm)

Xét ΔBAC có BD là phân giác

nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)

=>\(\dfrac{AD}{6}=\dfrac{CD}{10}\)

=>\(\dfrac{AD}{3}=\dfrac{CD}{5}\)

mà AD+CD=AC=8cm

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{AD}{3}=\dfrac{CD}{5}=\dfrac{AD+CD}{3+5}=\dfrac{8}{8}=1\)

=>\(AD=3\cdot1=3\left(cm\right);CD=5\cdot1=5\left(cm\right)\)

b: Xét ΔBAD vuông tại A và ΔBHI vuông tại H có

\(\widehat{ABD}=\widehat{HBI}\)

Do đó: ΔBAD~ΔBHI

=>\(\dfrac{BA}{BH}=\dfrac{BD}{BI}\)

=>\(BA\cdot BI=BD\cdot BH\)

c: Ta có: ΔBAD~ΔBHI

=>\(\widehat{BDA}=\widehat{BIH}\)

mà \(\widehat{BIH}=\widehat{AID}\)(hai góc đối đỉnh)

nên \(\widehat{AID}=\widehat{ADI}\)

=>ΔADI cân tại A

Answer 2

  

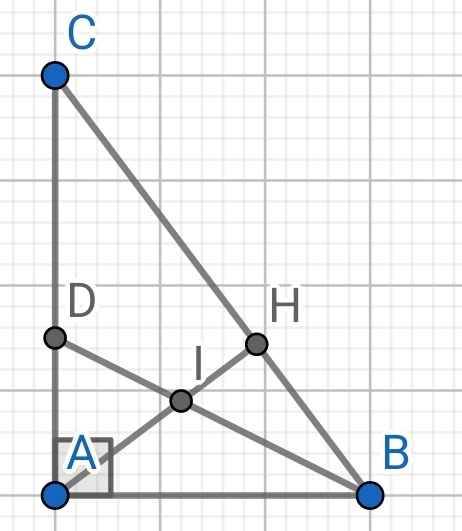
a) ∆ABC vuông tại A (gt)

⇒ BC² = AB² + AC² (Pythagore)

= 6² + 8²

= 100

⇒ BC = 10 (cm) 

Do BD là đường phân giác của ∆ABC (gt)

⇒ DA/DC = AB/BC

⇒ DA/AB = DC/BC

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

DA/AB = DC/BC = (DA + DC)/(AB + BC) = AC/(6 + 10) = 8/16 = 1/2

DA/AB = 1/2

⇒ DA = 1/2 . AB = 1/2 . 6 = 3 (cm)

DC/BC = 1/2 

⇒ DC = 1/2 . BC = 1/2 . 10 = 8 (cm)

b) Do BD là đường phân giác của ∆ABC (gt)

⇒ ∠ABD = ∠CBD

⇒ ∠ABD = ∠HBI

Xét hai tam giác vuông: ∆ABD và ∆HBI có:

∠ABD = ∠HBI (cmt)

⇒ ∆ABD ∽ ∆HBI (g-g)

⇒ AB/HB = BD/BI

⇒ AB.BI = BD.HB

c) Do ∆ABD ∽ ∆HBI (cmt)

⇒ ∠ADB = ∠HIB

⇒ ∠ADI = ∠HIB

Mà ∠HIB = ∠AID (đối đỉnh)

⇒ ∠ADI = ∠AID

⇒ ∆AID cân tại A