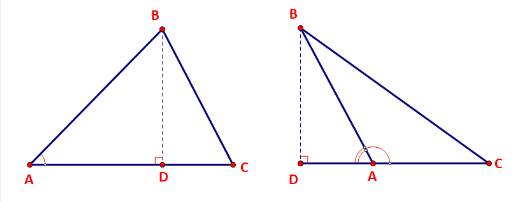
a) Xét tam giác vuông ABD vuông tại D ta có:
TH1: góc A nhọn
\(\sin A = \frac{{BD}}{{AB}} \Rightarrow BD = AB.\sin A\)
TH2: góc A tù
\(\sin A = \sin ({180^o} - A) = \frac{{BD}}{{AB}} \Rightarrow BD = AB.\sin A\)
Vậy \(BD = AB.\sin A\)
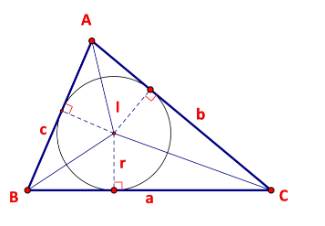
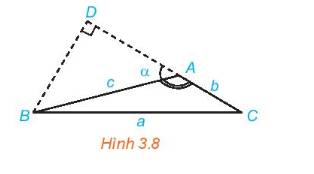
b) Ta có diện tích S của tam giác ABC là: \(S = \frac{1}{2}BD.AC\)
Mà \(BD = AB.\sin A = c.\sin A\); BC = a. Thế vào (*) ta được:
\(S = \frac{1}{2}c.\sin A.b\) hay \(S = \frac{1}{2}bc.\sin A.\)
Vậy diện tích S của tam giác ABC theo b, c, sin A là \(S = \frac{1}{2}bc.\sin A.\)