Question

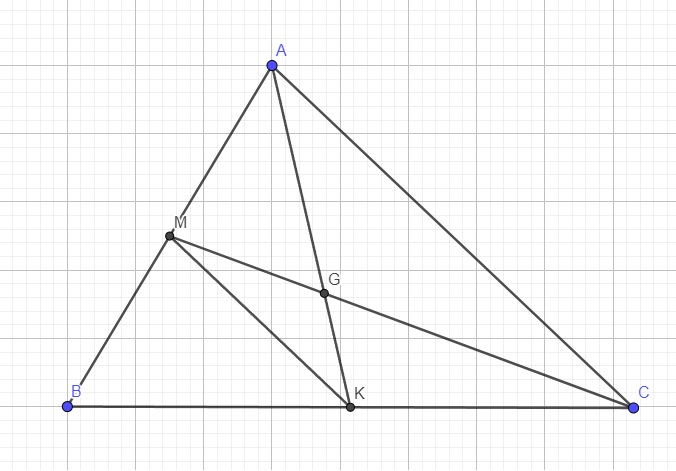
Cho tam giác ABC và G là điểm thuộc miền trong tam giác. Tia AG cắt BC tại
K và tia CG cắt AB tại M. Biết AG =2GK và CG = 2GM. Chứng minh rằng G là trọng
tâm của tam giác ABC

Answer 1

Từ giả thiết \(AG=2GK\Rightarrow\dfrac{GK}{AG}=\dfrac{1}{2}\)

\(CG=2GM\Rightarrow\dfrac{GM}{CG}=\dfrac{1}{2}\)

\(\Rightarrow\dfrac{GM}{CG}=\dfrac{GK}{GA}\)

\(\Rightarrow MK||AC\) (định lý Talet đảo)

\(\Rightarrow\dfrac{MK}{AC}=\dfrac{GM}{CG}=\dfrac{1}{2}\)

Do \(\left\{{}\begin{matrix}MK||AC\\MK=\dfrac{1}{2}AC\end{matrix}\right.\) \(\Rightarrow MK\) là đường trung bình tam giác ABC

\(\Rightarrow\) M là trung điểm AC và K là trung điểm AB

\(\Rightarrow G\) là giao điểm 2 trung tuyến AK và CM nên G là trọng tâm tam giác ABC

Answer 2