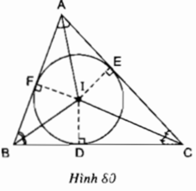
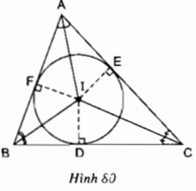
Cho tam giác ABC, góc A > 900. Gọi D,E,F theo thứ tự là chân các đường cao kẻ từ A,B,C. Chứng minh rằng
a Các điểm A,D,B,E cùng nằm trên một đường tròn
b Các điểm A,D,C,F cùng nằm trên 1 đường tròn
c Các điểm B,C,E,F cùng nằm trên 1 đường tròn
(Chỉ được sử dụng kiến thức của học kì một, tại mình chưa học đến chứng minh đường tròn nột tiếp nên các bn thông cảm)
a: Ta có: ΔADB vuông tại D
=>D,A,B cùng nằm trên đường tròn đường kính AB(1)
Ta có: ΔEAB vuông tại E
=>E,A,B cùng nằm trên đường tròn đường kính AB(2)
Từ (1),(2) suy ra D,A,E,B cùng thuộc một đường tròn
b: Ta có: ΔADC vuông tại D
=>D nằm trên đường tròn đường kính AC(3)
Ta có: ΔCFA vuông tại F
=>F nằm trên đường tròn đường kính AC(4)
Từ (3) và (4) suy ra C,F,A,D cùng thuộc một đường tròn
c: Ta có:ΔCEB vuông tại E
=>E nằm trên đường tròn đường kính CB(5)
ta có: ΔCFB vuông tại F
=>F nằm trên đường tròn đường kính CB(6)
Từ (5),(6) suy ra B,C,F,E cùng thuộc một đường tròn