Bài 6: Trường hợp đồng dạng thứ hai
Các câu hỏi tương tự
cho tam giác ABC vuông tại A có AB = 6 cm BC = 10 cm vẽ đường cao AH của tam giác ABC( H thuộc BC )
1 cm tam giác ABC đồng dạng tam giác hba
2 cm AB bình = BC.BH áp dụng tính HB
3 tia phân giác của góc B cắt AC tại K cmr AK.AC=AH.KC
Cho tam giác ABC biết AB=6cm, BC=10cm, CA=8cm. Trên AB lấy M sao cho AM=4cm, trên AC lấy N sao cho AN=3cm. CMR tam giác ABC đồng dạng với tam giác ANMGiúp mình với ạ, mình đang cần gấp, pờ lítttt
Cho tam giác ABC có 3 góc nhọn và 3 đường cao AD, BE, CF cắt nhau tại H. Chứng minh
1, BD.BC= BF.BA
2, Tam giác BDF đồng dạng với tam giác BAC và góc BDF = góc BAC
3, góc CDE = góc BAC
4, DH là phân giác của góc FDE
cho góc xOy với tia Ot là tia phân giác , trên tia Ox lấy điểm A sao cho OA =4 cm , trên tia Oy chọn điểm B sao cho OB=6cm , trên tia Ot chọn 2 điểm E và F sao cho OE= 2cm ,OF=3cm ; a)Chứng minh tam giác AOE đồng dạng vs tam giác BOF ; b)Cho AE =2,4 , BF =?
Cho tam giác ABC vuông tại A đường cao AH chứng minh rằng a. Tam giác ABC đồng dạng với tam giác AC b. AB. AC = AH. BC c. 1/Ah^2 = 1/AB^2 + 1/AC^2
Cho tam giác ABC có AB=4cm, AC=5cm, BC=6cm. CMR: góc A=2 lần góc C
Cho tam giác ABC có \(\widehat{A}=60^0;AB=6cm,AC=9cm\), (h.24)
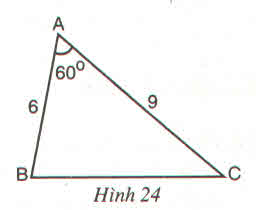
a) Dựng tam giác đồng dạng với tam giác ABC theo tỉ số đồng dạng \(k=\dfrac{1}{3}\)
b) Hãy nêu một vài cách dựng khác và vẽ hình trong từng trường hợp cụ thể ?
Trên một cạnh của góc xOy \(\left(\widehat{xOy}\ne180^0\right)\), đặt các đoạn thẳng OA = 5cm, OB = 16 cm. Trên cạnh thứ hai của góc đó, đặt các đoạn thẳng OC = 8cm, OD = 10cm
a) Chứng minh hai tam giác OCB và OAD đồng dạng
b) Gọi giao điểm của các cạnh AD và BC là I, chứng minh rằng hai tam giác IAB và ICD có các góc bằng nhau từng đôi một
cho tam giác ABC. trên các cạnh BC, CA, AB lấy lần lượt các điểm m,n, p sao cho am, bn, cp đồng quy tại o. qua a và c vẽ các đường thẳng song song với bo cắt co, oa lần lượt ở e và f.
a) chứng minh: tam giác FCM đồng dạng với tam giác OBM và tam giác PAE đồng dạng với tam giác PBO.
b) chứng minh: MB/MC . NC/NA . PA/PB = 1











