Các câu hỏi tương tự
Cho Δ ABC có AB=AC. Kẻ BD vuông góc AC, CE vuông góc AB (D ϵ AC; E ϵ AB). Gọi O là giao điểm của BD và CE. Chứng minh:
a) Δ ABD = Δ ACE
b) BD = CE
c) Δ AOE = Δ AOD
d) Δ OEB = Δ ODC
e) AO là tia phân giác của góc BAC
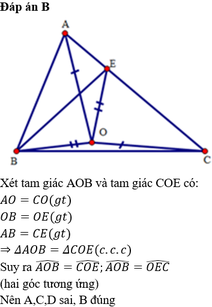
Cho tam giác ABC có ABAC. Gọi E sao cho E thuốc AC. Gọi O là một điểm nằm trong tam giác sao cho OAOC, OBOE. Khi đó A.
∆
A
O
B
∆
C
E
O
B.
∆
A
O
B
∆
C
O
E
C.
A
O
B
^
O
E
C...
Đọc tiếp
Cho tam giác ABC có AB<AC. Gọi E sao cho E thuốc AC. Gọi O là một điểm nằm trong tam giác sao cho OA=OC, OB=OE. Khi đó
A. ∆ A O B = ∆ C E O
B. ∆ A O B = ∆ C O E
C. A O B ^ = O E C ^
D. A B O ^ = O C E ^
1. Cho Δ ABC có đường trung tuyến AD. Lấy điểm G trên đoạn AD sao cho AG2.GD, Gọi E là trung điểm của ACChứng Minh AG2/4AD ( 2 phần 3 ) và B,G,E thẳng hàng2. Trên đường trung tuyến AD của Δ ABC, lấy hai điểm I và G sao cho AIIGGD Gọi E là trung điểm ACA) chứng minh B,G,E thằng hàng, so sánh BE và GEb) CI cắt GE ở O, Điểm O là gì của Δ ACG ? Chứng minh BE 9 . OE3. Cho Δ ABC. Trên BC lấy điểm T sao cho BT 2.TC kéo dài từ A đến C thêm một đoạn CDCAa) Điểm T là gì của ΔABD ?b) DT cắt AB tại E. Chứng...
Đọc tiếp
1. Cho Δ ABC có đường trung tuyến AD. Lấy điểm G trên đoạn AD sao cho AG=2.GD, Gọi E là trung điểm của AC
Chứng Minh AG=2/4AD ( 2 phần 3 ) và B,G,E thẳng hàng
2. Trên đường trung tuyến AD của Δ ABC, lấy hai điểm I và G sao cho AI=IG=GD Gọi E là trung điểm AC
A) chứng minh B,G,E thằng hàng, so sánh BE và GE
b) CI cắt GE ở O, Điểm O là gì của Δ ACG ? Chứng minh BE= 9 . OE
3. Cho Δ ABC. Trên BC lấy điểm T sao cho BT= 2.TC kéo dài từ A đến C thêm một đoạn CD=CA
a) Điểm T là gì của ΔABD ?
b) DT cắt AB tại E. Chứng minh E là trung điểm AB
cao nhân nào giúp mình với gấp lắm
Cho tam giác ABC có AC > AB. Trên cạnh AC lấy điểm E sao cho CE = AB. Gọi O là 1 điểm sao cho OA = OC, OB = OE
a/ CMR tam giác AOB = tam giác COE
b/ So sánh góc OAB và góc OCA
Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho AC = BD.
a) Chứng minh: AD = BC.
b) Gọi E là giao điểm AD và BC. Chứng minh: Δ EAC = Δ EBD.
c) Gọi I là trung điểm của CD. Chứng minh ba điểm O,E,I thẳng hàng
Cho tam giác ABC vuông tại A có , đường cao AH. Trên tia đối của tia HB lấy điểm M sao cho HM HB.
a) Chứng minh rằng HB HC.
b) Chứng minh rằng Δ∆AHB Δ∆AHM. Từ đó suy ra Δ∆ABM là tam giác đều.
c) Gọi N là trung điểm của AC và O là giao điểm của AM và BN. Biết AB 4 cm, tính độ dài đoạn thẳng AO.
Đọc tiếp
Cho tam giác ABC vuông tại A có , đường cao AH. Trên tia đối của tia HB lấy điểm M sao cho HM = HB.
a) Chứng minh rằng HB < HC.
b) Chứng minh rằng AHB = AHM. Từ đó suy ra ABM là tam giác đều.
c) Gọi N là trung điểm của AC và O là giao điểm của AM và BN. Biết AB = 4 cm, tính độ dài đoạn thẳng AO.
cho tam giác ABC có AC>AB. Trên cạnh AC lấy E sao cho CE=AB. Gọi O là 1 điểm sao cho OA= OC, OB= OE. Chứng minh:
a, tam giác AOB= tam giác COE
b, so sánh góc OAB và góc OCA
(VẼ HÌNH)
1.Cho tam giác ABC có AC AB. Trên cạnh AC lấy điểm E sao cho CE AB. Gọi O là một điểm sao cho OA OC, OB OE. Chứng minh:a) Tam giác AOB COEb) So sánh góc OAB và góc OCA?2. Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA OB. Từ A kẻ đường thẳng vuông góc với Ox cắt Oy ở E, từ B kẻ đường thẳng vuông góc với Oy cắt Ox ở F. AE và BF cắt nhau tại I. Chứng minh:a) AE BFb) Tam giác AFI BEIc) OI là tia phân giác của góc AOB3. Cho tam giác ABC, D là trung điểm của AB, v...
Đọc tiếp
1.Cho tam giác ABC có AC > AB. Trên cạnh AC lấy điểm E sao cho CE = AB. Gọi O là một điểm sao cho OA = OC, OB = OE. Chứng minh:
a) Tam giác AOB = COE
b) So sánh góc OAB và góc OCA?
2. Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Từ A kẻ đường thẳng vuông góc với Ox cắt Oy ở E, từ B kẻ đường thẳng vuông góc với Oy cắt Ox ở F. AE và BF cắt nhau tại I. Chứng minh:
a) AE = BF
b) Tam giác AFI = BEI
c) OI là tia phân giác của góc AOB
3. Cho tam giác ABC, D là trung điểm của AB, vẽ các tia Ax và By vuông góc với AB. Gọi C là điểm thuộc tia Ax. Đường vuông góc OC tại O cắt tia By ở D. Chứng minh rằng:
a) AD = EF
b) Tam giác ADE = EFC
c) AE = EC
Cho tam giác ABC có AB = BC = AC. Gọi O là một điểm bất kỳ nằm trong tam giác sao cho OA = OB = OC. Chứng minh rằng O là giao điểm 3 tia phân giác của các góc A; B; C.