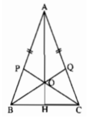
Cho tam giác ABC cân tại A. CP,BQ là các tia phân giác trong của tam giác ABC (\(P\in\) AB, \(Q\in\) AC). Gọi O là giao điểm của CP và BQ.
a) Chứng minh tam giác OBC là tam giác cân.
b) Chứng minh đường thẳng AO vuông góc với BC.
c) Chứng minh CP = BQ.
d) Tm giác ABQ là tam giác gì?Vì sao?
Mình cần gấp ạ ![]()

a, Ta có: `\hat{OBC}=\hat{ABQ}=\frac{\hat{ABC}}{2}`
`\hat{OCB}=\hat{ACP}=\frac{\hat{ACB}}{2}`
mà `\hat{ABC}=\hat{ACB}`
`=>\hat{OBC}=\hat{OCB}`
`=>\triangleOBC` cân tại `O` `(đpcm)`
b, Gọi `D` là trung điểm của `BC`
`\triangleABC` cân tại `A` nên `AD` là đường trung trực của `BC`
`\triangleOBC` cân tại `O` nên `OD` là đường trung trực của `BC`
`=> A,O,D` thẳng hàng
`=>AO \bot BC` `(đpcm)`
c, Xét `\triangleBCP` và `\triangleCBQ` có:
`\hat{CBP}=\hat{BCQ}`
`BC` cạnh chung
`\hat{BCP}=\hat{CBQ}`
`=>\triangleBCP=\triangleCBQ(g.c.g)`
`=>CP=BQ` `(đpcm)`