Question

Cho (O) đường kính AB.Hai điểm I,K thuộc AB sao cho OI=OK,M bất kì thuộc (O).MO,MI,MK cắt (O) lần lượt tại E,C,D cắt AB tại F,EI cắt DF tại N,MI cắt EF tại H.CMR

a)ENCH nội tiếp

b)EF là tiếp tuyến

Answer 1

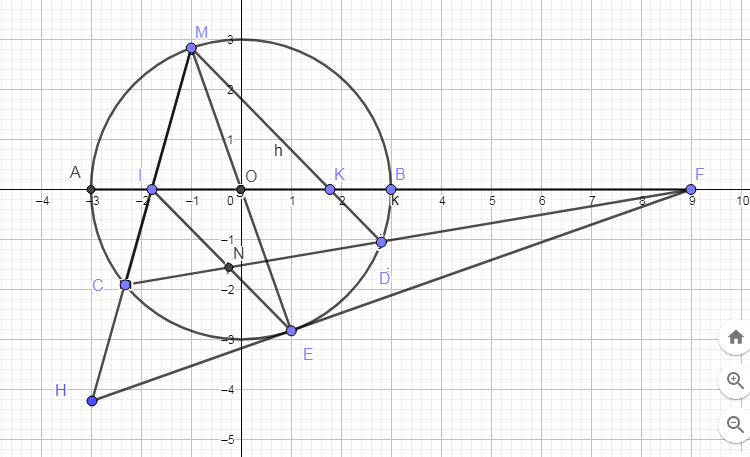
hình tự vẽ nhe

a, \(DE\perp MD\)( ME là đường kính )

mà \(\left\{{}\begin{matrix}ED//HN\left(cmt\right)\\MD//EI\left(EIMK:hbh\right)\end{matrix}\right.\)

=> HN⊥EI 

mà EC ⊥MC ( ME là đường kính)

khi đó : CN cùng nhìn với EH dưới góc vuông

Vậy ENCH nội tiếp.( đpcm)

 

b, gọi điểm giao nhau giữa FD và MH là G

ta có :

góc HNG = góc HEG ( ENCH nội tiếp)

góc EDG = góc HNG ( đồng vị)

từ đó suy ra:

góc HEG = góc EDG

<=> góc HEG là góc giữa tiếp tuyến và dây cung 

hay nói cách khác: EF là tiếp tuyến của (O)( đpcm)