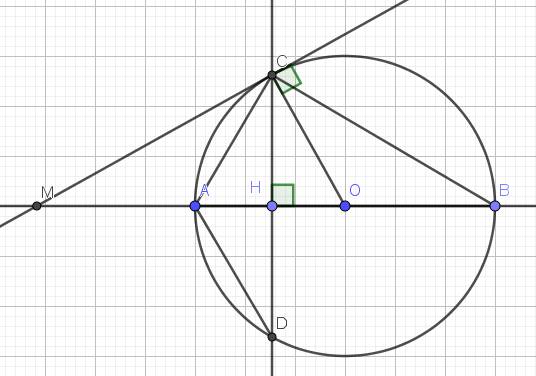
Lời giải:
Vì $CM$ là tiếp tuyến của $(O)$ nên:
$\widehat{MCA}=\widehat{CDA}(1)$ (góc nt tạo bởi tiếp tuyến và dây cung thì bằng góc nt chắn cung đó)
$OC=OD=R, OA\perp CD$ tại $H$ nên $OA$ là đường trung trực của $CD$
$\Rightarrow AC=AD$
$\Rightarrow \triangle CAD$ cân tại $A$
$\Rightarrow \widehat{CDA}=\widehat{ACD}(2)$
Từ $(1); (2)\Rightarrow \widehat{MCA}=\widehat{ACD}$
$\Rightarrow CA$ là phân giác trong $\widehat{MCH}$
$\Rightarrow \frac{MA}{AH}=\frac{MC}{CH}$ (tính chất tia phân giác) $(*)$
Mặt khác:
$\widehat{ACB}=90^0$ (góc nt chắn nửa đt)
$\Rightarrow AC\perp CB$
$\Rightarrow CB$ là phân giác ngoài $\widehat{MCH}$
$\Rightarrow \frac{MB}{BH}=\frac{MC}{CH}(**)$
Từ $(*); (**)\Rightarrow \frac{MA}{AH}=\frac{MB}{BH}$
$\Rightarrow MA.BH=MB.AH$
Ta có đpcm.