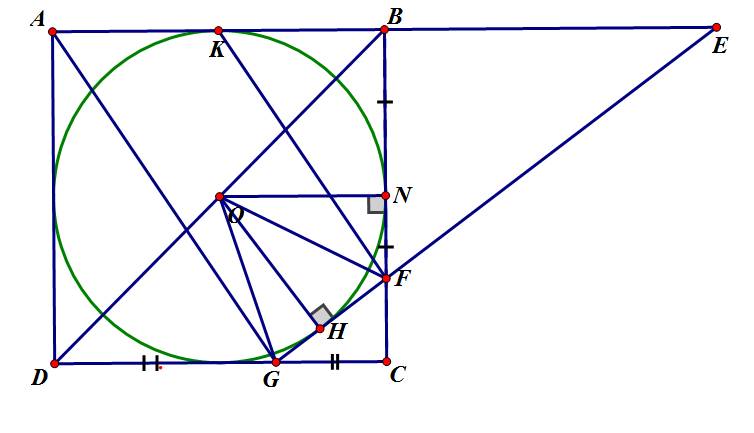
*GF cắt AB tại E.
- \(CF=\dfrac{1}{2}CN=\dfrac{1}{2}.\dfrac{1}{2}BC=\dfrac{1}{4}BC\)
CG// BE \(\Rightarrow\dfrac{EF}{EG}=\dfrac{BF}{BC}=\dfrac{3}{4}\)
KF// AG \(\Rightarrow\dfrac{EK}{AE}=\dfrac{EF}{EG}=\dfrac{3}{4}\)
\(\Rightarrow\dfrac{AK}{AE}=\dfrac{1}{4}\Rightarrow\dfrac{AB}{AE}=\dfrac{1}{2}\Rightarrow AB=BE\)
CG// BE \(\Rightarrow\dfrac{CG}{BE}=\dfrac{CF}{BF}=\dfrac{1}{3}\Rightarrow CG=\dfrac{AB}{3}\)
- O là tâm hình vuông \(\Rightarrow O\in CD\).
- ΔBCD vuông cân tại C \(\Rightarrow BD=BC\sqrt{2}\)
\(\Rightarrow OD=OB=\dfrac{\sqrt{2}}{2}BC\)
\(\Rightarrow OD.OB=\dfrac{1}{2}BC^2\) mà \(DG.BF=\dfrac{2}{3}BC.\dfrac{3}{4}BC=\dfrac{1}{2}BC^2\)
\(\Rightarrow OD.OB=DG.BF\)
\(\Rightarrow\dfrac{DG}{OB}=\dfrac{OD}{BF}\).
- ΔODG và ΔFBO: \(\widehat{ODG}=\widehat{FBO}=45^0;\dfrac{DG}{OB}=\dfrac{OD}{BF}\)
\(\Rightarrow\)ΔODG∼ΔFBO (c-g-c).
\(\Rightarrow\widehat{DOG}=\widehat{BFO}\)
\(\widehat{GOF}=180^0-\widehat{DOG}-\widehat{BOF}=180^0-\widehat{BFO}-\widehat{BOF}=\widehat{OBF}=45^0\)
Mặt khác: \(\dfrac{OG}{OF}=\dfrac{OD}{BF}\Rightarrow\dfrac{OG}{OF}=\dfrac{OB}{BF}\)
ΔOGF và ΔBOF: \(\widehat{GOF}=\widehat{OBF}=45^0\); \(\dfrac{OG}{OB}=\dfrac{OF}{BF}\)
\(\Rightarrow\)ΔOGF∼ ΔBOF (c-g-c).
\(\Rightarrow\widehat{OFG}=\widehat{BFO}\).
- ΔOHF và ΔONF: \(\widehat{OFH}=\widehat{OFN}\), \(\widehat{OHF}=\widehat{ONF}=90^0\); OF là cạnh chung.
\(\Rightarrow\)ΔOHF= ΔONF (ch-gn).
\(\Rightarrow OH=ON\). Mà \(N\in\) đường tròn tâm O nội tiếp hình vuông.
\(\Rightarrow H\in\) đường tròn tâm O nội tiếp hình vuông.
Mà \(GF\perp OH\) tại H \(\Rightarrowđpcm\)