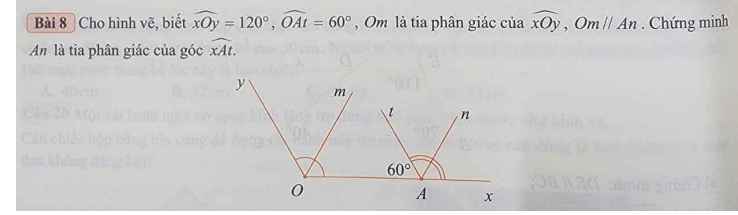
Ta có :
\(\widehat{tAx}=180^o-\widehat{OAt}=180^o-60^o=120^o\)
mà \(\widehat{tAx}=\widehat{tAn}+\widehat{nAx}=120^o\)
\(\widehat{nAx}=\widehat{mOx}=\widehat{yOm}=\dfrac{120^o}{2}=60^o\) ( Om là phân giác và \(On//An\))
\(\Rightarrow\widehat{tAx}=\widehat{nAx}=60^o\)
\(\Rightarrow An\) là phân giác \(\widehat{xAt}\)
Ta có: \(\widehat{xAt}+\widehat{tAO}=180^0\)(hai góc kề bù)
=>\(\widehat{xAt}=180^0-60^0=120^0\)
Om là phân giác của góc xOy
=>\(\widehat{xOm}=\widehat{yOm}=\dfrac{\widehat{xOy}}{2}=\dfrac{120^0}{2}=60^0\)
Om//An
=>\(\widehat{xAn}=\widehat{xOm}\)(hai góc đồng vị)
=>\(\widehat{xAn}=60^0\)
Vì \(\widehat{xAn}< \widehat{xAt}\left(60^0< 120^0\right)\)
nên tia An nằm giữa hai tia Ax và At
=>\(\widehat{xAn}+\widehat{tAn}=\widehat{xAt}\)
=>\(\widehat{tAn}=120^0-60^0=60^0\)
ta có: tia An nằm giữa hai tia Ax và At
mà \(\widehat{nAx}=\widehat{nAt}\left(=60^0\right)\)
nên An là phân giác của góc xAt