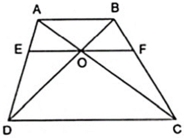
Sửa đề: lần lượt cắt AD,BC tại E và H
Xét ΔADC có OE//DC
nên \(\dfrac{OE}{DC}=\dfrac{AE}{AD}\left(1\right)\)
Xét ΔBDC có OH//DC
nên \(\dfrac{OH}{DC}=\dfrac{BH}{BC}\left(2\right)\)
Xét hình thang ABCD có EH//AB//CD
nên \(\dfrac{AE}{ED}=\dfrac{BH}{HC}\)
=>\(\dfrac{ED}{EA}=\dfrac{CH}{HB}\)
=>\(\dfrac{ED+EA}{EA}=\dfrac{CH+HB}{HB}\)
=>\(\dfrac{AD}{EA}=\dfrac{CB}{HB}\)
=>\(\dfrac{AE}{AD}=\dfrac{BH}{BC}\left(3\right)\)
Từ (1),(2),(3) suy ra OE=OH