Các câu hỏi tương tự
hình thang ABCD có đáy AB, CD. cho AB=CD, CMR: AD//BC, AD=BC
Cho hình thang ABCD có đáy AB và CD biết AB = CD . C/m BC=AD và BC//AD
CHo hình thang ABCD có đáy AB , CD . biết AB = CD . C/m BC =AD và BC // AD
cho hình thang ABCD(AB//CD).CMR: nếu AC+BC=AD+DB thì ABCD là hình thang cân
Cho hình thang ABCD(AB||CD). CMR: nếu AC+BC=AD+BD thì hình thang ABCD là hình thang cân
24 tháng 9 2020 lúc 20:59
Hình thang ABCD với đáy lớn AD và đáy nhỏ BC, AC = CD. Đường thẳng đối xứng với BC qua AD cắt AC tại E. CMR: AB chia đôi ED
cho hình thang ABCD ( AB // CD ). Gọi E là trung điểm của AB, F là trung điểm của CD, O là trung điểm của EF. Qua O kể đường thẳng ss với CD cắt AD và BC theo thứ tự tại M và N.
a. CMR: M là trung điểm của AD, N là trung điểm của BC
b. CMR: OM=ON
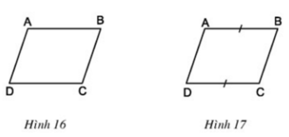
Hình thang ABCD có đáy AB, CD.
a) Cho biết AD // BC (h.16). Chứng minh rằng AD = BC, AB = CD.
b) Cho biết AB = CD (h.17). Chứng minh rằng AD // BC, AD = BC.
cho hình thang ABCD có đáy AB và CD .C/m BC=AD và BC//AD