Chứng minh được: ∆DBC:∆BAD => D B C ^ = B A D ^
=> s đ D B C ⏜ = 1 2 s đ B m D ⏜
=> BC là tiếp tuyến của (O)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
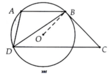
Cho hình thang ABCD (AB//CD), có BD^2=AB.CD. CMR: Đường tròn ngoại tiếp tam giác ABD tiếp xúc với BC.
cho hình thang ABCD ( AB //CD)
Có : BD^2 = AB.CD
CMR : Đường tròn ngoại tiếp tam giác ABD tiếp xúc với BC
Cho hình thang vuông ABCD có ∠ A = ∠ D = 90 ° , AB = 4cm, BC = 13cm, CD = 9cm. Chứng minh rằng đường thẳng AD tiếp xúc với đường tròn có đường kính là BC
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại M. Kẻ tiếp tuyến chung ngoài AB và CD của hai đường tròn (A và D ∈ (O), C và B ∈ (O’)) . Chứng minh rằng:
a) Tam giác AMB là tam giác vuông
b) Đường tròn đường kính AB tiếp xúc với OO’
c) Tứ giác OABO’ là hình thang vuông
d) Tứ giác ABCD là hình thang cân
1)Cho tam giác đều ABC có đường cao AH. Trên cạnh BC lấy M bất kì. Từ M kẻ MP, MQ theo thứ tự vuông góc với AB, AC.
a) tìm tâm O của đường tròn ngoại tiếp tứ giác APMQ
b) CM: OH vuông góc với PQ.
2) Cho hình thang vuông( ^A=D=90o), AB=4cm, BC=13cm, CD= 9cm. Chứng minh rằng đường thẳng AD tiếp xúc với đường tròn có đường kính BC
Tứ giác ABCD có đường tròn (O) đường kính AB tiếp xúc CD. Chứng minh đường tròn (I) đường kính CD tiếp xúc AB <=>AD//BC.
Cho hình thoi ABCD có B= 60 độ. 1 đường thẳng qua D không cắt hình thoi nhưng cắt các đường thẳng AB và BC lần lượt tại E và F. Gọi M giao điểm AF, CE. Chứng minh AD tiếp xúc với đường tròn ngoại tiếp tam giác MDF.
13 tháng 8 2023 lúc 11:28
Cho tam giác ABC có đường tròn bàng tiếp góc A tiếp xúc với BC tại D. Chứng minh rằng đường tròn bàng tiếp góc A của hai tam giác ABD, ACD tiếp xúc với AD tại một điểm chung.
13 tháng 8 2023 lúc 11:33
Cho tam giác ABC có đường tròn bàng tiếp góc A tiếp xúc với BC tại D. Chứng minh rằng đường tròn bàng tiếp góc A của hai tam giác ABD, ACD tiếp xúc với AD tại một điểm chung.