Question

Cho hình thang ABCD (AB // CD), AC cắt BD tại O. Kẻ OM // CD,cắt AD tại M, biết CD = 9cm, MO = 3cm. Tính AB.

Answer 1

Xét ΔADC có OM//DC
nên \(\dfrac{OM}{DC}=\dfrac{AO}{AC}\)

=>\(\dfrac{AO}{AC}=\dfrac{3}{9}=\dfrac{1}{3}\)

=>AC=3AO

Xét ΔOAB và ΔOCD có

\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)

\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)

Do đó: ΔOAB~ΔOCD

=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)

=>\(\dfrac{OA}{OC+OA}=\dfrac{OB}{OD+OB}\)

=>\(\dfrac{AO}{AC}=\dfrac{BO}{BD}\)

=>\(\dfrac{BO}{BD}=\dfrac{1}{3}\)

=>\(\dfrac{DO}{DB}=\dfrac{2}{3}\)

Xét ΔDAB có OM//AB

nên \(\dfrac{OM}{AB}=\dfrac{DO}{DB}\)

=>\(\dfrac{3}{AB}=\dfrac{2}{3}\)

=>\(AB=3\cdot\dfrac{3}{2}=4,5\left(cm\right)\)

 

Answer 2

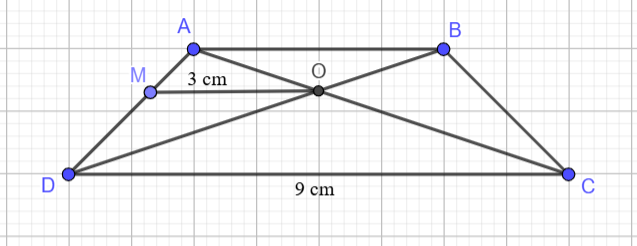
Xét `\triangle ADC` có: `MO //// DC`

   `=> [MO]/[DC] = [MA]/[AD]` (Hệ quả của định lý Ta-lét)

   `=>[MA]/[AD] = 3/9 = 1/3`

Hay `[DM]/[DA] = 2/3`

Xét `\triangle ADB` có: `MO //// AB`

   `=>[MO]/[AB] = [DM]/[DA]` (Hệ quả của định lý Ta-lét)

   `=>3/[AB] = 2/3`

   `=>AB = 9/2 (cm)`.