Question

Cho hình lập phương ABCD.A’B’C’D’. Gọi beta là số đo của góc nhị diện [B,A’C’,B’]. Giá trị tan beta bằng ?

Answer 1

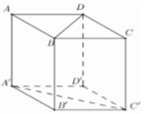
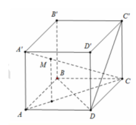
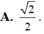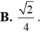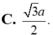Kẻ BH vuông A'C' 

Ta có A'C' vuông B'H ; A'C' vuông BB' 

=> A'C' vuông (B'BH) 

(B'BH) giao (BA'C') = BH 

(B'BH) giao (A'C'B') = B'H 

=> góc nhị diện [B;A'C',B'] là góc ^BHB' 

Cho các cạnh hình lập phương là a 

ADHT \(\dfrac{1}{B'H^2}=\dfrac{1}{A'B'^2}+\dfrac{1}{B'C'^2}=\dfrac{1}{a^2}+\dfrac{1}{a^2}=\dfrac{2}{a^2}\Rightarrow B'H=\dfrac{a}{\sqrt{2}}\)

tan^BHB' = \(\dfrac{a}{\dfrac{a}{\sqrt{2}}}=\sqrt{2}\)