Question

Cho hình lăng trụ ABCA’B’C’ với ABC là tam giác vuông tại A, AB = 2AC = 2a. AA’ vuông góc với mặt phẳng (ABC), AA’ = 3a. a) Chứng minh AC vuông góc mp(AA’B’B) b) Xác định và tính số đo góc giữa đường thẳng BC’ và mp(ABC)

Answer 1

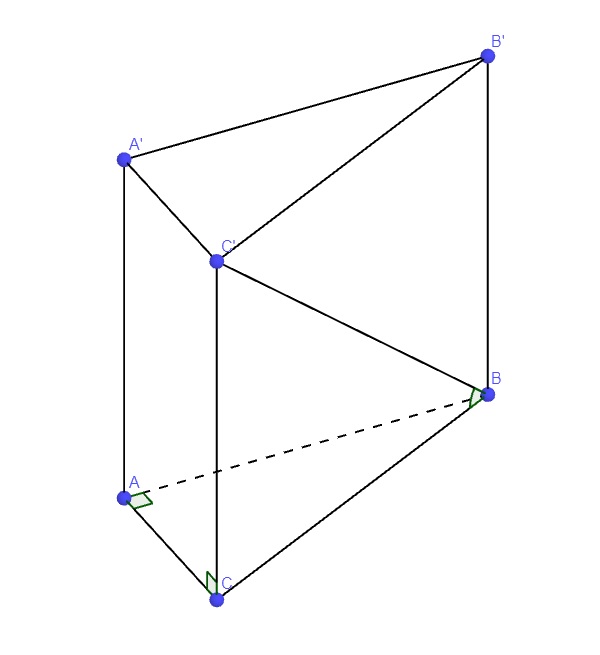
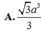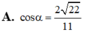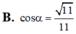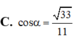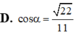\(\left\{{}\begin{matrix}A'A\perp\left(ABC\right)\Rightarrow A'A\perp AC\\AC\perp AB\left(gt\right)\end{matrix}\right.\)

\(\Rightarrow AC\perp\left(ABB'A'\right)\)

b.

\(C'C||A'A\Rightarrow C'C\perp\left(ABC\right)\)

\(\Rightarrow BC\) là hình chiếu vuông góc của BC' lên (ABC)

\(\Rightarrow\widehat{C'BC}\) là góc giữa BC' và (ABC)

\(BC=\sqrt{AB^2+AC^2}=a\sqrt{5}\)

\(tan\widehat{C'BC}=\dfrac{C'C}{BC}=\dfrac{3a}{a\sqrt{5}}=\dfrac{3}{\sqrt{5}}\)

\(\Rightarrow\widehat{C'BC}\approx53^018'\)

Answer 2