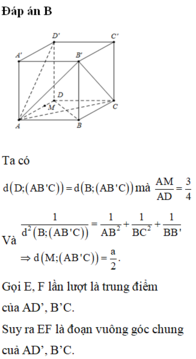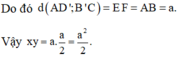Các câu hỏi tương tự
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB a, AD 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng
45
0
.Gọi M là trung điểm của SD. Tính theo a khoảng cách d từ điểm M đến mặt phẳng (SAC) A.
d
a
1315
89
B.
d...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB =a, AD = 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45 0 .Gọi M là trung điểm của SD. Tính theo a khoảng cách d từ điểm M đến mặt phẳng (SAC)
A. d = a 1315 89
B. d = a 1513 89
C. d = 2 a 1315 89
D. d = 2 a 1513 89
1. Cho tứ diện ABCD có AD vuông góc (ABC), AD=a√3. Góc giữa (ABC) và (DBC) bằng 60⁰. Gọi M là trung điểm AD. Tính khoảng cách từ M đến (BCD). 2. Cho hình chóp S.ABCD có SA vuông góc (ABCD), đáy ABCD là hình chữ nhật tâm O. Biết AD=2a, SA=a. Khoảng cách từ O đến (SCD) bằng
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AA 2a, AD 4a. Gọi M là trung điểm của cạnh AD. Tính khoảng cách d từ giữa hai đường thẳng A’B’ và C’M
A
.
d
2
a
2
B
.
d
a
2
C
.
d
2
a
D...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AA' = 2a, AD = 4a. Gọi M là trung điểm của cạnh AD. Tính khoảng cách d từ giữa hai đường thẳng A’B’ và C’M
A . d = 2 a 2
B . d = a 2
C . d = 2 a
D . d = 3 a
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AA’ 2a, AD 4a. Gọi M là trung điểm của cạnh AD. Tính khoảng cách d từ giữa hai đường thẳng A’B’ và C’M.
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AA’ = 2a, AD = 4a. Gọi M là trung điểm của cạnh AD. Tính khoảng cách d từ giữa hai đường thẳng A’B’ và C’M.
![]()
![]()
![]()
![]()
cho hình chóp SABCD đáy ABCD là hình chữ nhật AB= a ,AD=2a,SA=SB=SC=SD=2a gọi O là giao điểm của AC và BD
a chứng minh mặt phẳng SAC vuông góc với mặt phẳng ABCD
b tính khoảng cách từ O->mặt phẳng SCD
c gọi M,N lần lượt là trung điểm của các cạnh SA và BC tính sin góc MN,CSBD
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a, AD 2a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ D đến (SBC) bằng
2
a
3
. Tính khoảng cách giữa hai đường thẳng SB và AC.
A
.
a
10
10
B
.
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ D đến (SBC) bằng 2 a 3 . Tính khoảng cách giữa hai đường thẳng SB và AC.
A . a 10 10
B . a 10 5
C . 2 a 10 5
D . 2 a 5 5
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB a, AD 2a, AA’ 3a Gọi M, N, P lần lượt là trung điểm của BC, C’D’ và DD’. Tính khoảng cách từ A đến mp (MNP). A.
15
22
a
B.
9
11
a
C.
3
4
a
D.
15
11
a
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, AD =2a, AA’= 3a Gọi M, N, P lần lượt là trung điểm của BC, C’D’ và DD’. Tính khoảng cách từ A đến mp (MNP).
A. 15 22 a
B. 9 11 a
C. 3 4 a
D. 15 11 a
cho hình tứ diện ABCD có AB,AC,AD đôi một vuông góc và AB=AC=AD=5cm gọi M là trung điểm BC a) chứng minh BC vuông góc ADM b) tính khoảng cách từ điểm A đén BCD C) tính góc giữa đường thẳng DM và mặt phẳng ABC
Cho lăng trụ ABCD. A’B’C’D’ có đáy ABCD là hình chữ nhật với AB a, AD
a
3
Hình chiếu vuông góc của A lên (ABCD) trùng với giao điểm của AC và BD. Tính khoảng cách từ điểm B đến mặt phẳng (A’BD) A.
a
3
B.
a
2
C.
a
3
2
D. ...
Đọc tiếp
Cho lăng trụ ABCD. A’B’C’D’ có đáy ABCD là hình chữ nhật với AB =a, AD = a 3 Hình chiếu vuông góc của A' lên (ABCD) trùng với giao điểm của AC và BD. Tính khoảng cách từ điểm B' đến mặt phẳng (A’BD)
A. a 3
B. a 2
C. a 3 2
D. a 3 6