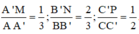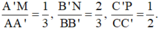Question

cho hình hộp ABCD.A'B'C'D'

a) cùng phương \(\overrightarrow{BC}\)

b) cùng hướng \(\overrightarrow{BB'}\)

c) bằng \(\overrightarrow{OB}\)

d) \(\overrightarrow{CD}+\overrightarrow{BB'}\)

e) \(\overrightarrow{CO}-\overrightarrow{CA'}\)

f) \(\overrightarrow{DD'}+\overrightarrow{DB}\)

g) \(\overrightarrow{BB'}+\overrightarrow{BA}+\overrightarrow{BB'}\)

h) \(\overrightarrow{C'A}+\overrightarrow{C'B}+\overrightarrow{C'D}\)

i) \(\overrightarrow{IA'}+\overrightarrow{IB'}+\overrightarrow{IC'}+\overrightarrow{ID'}\)

Answer 1

a: ABCD.A'B'C'D là hình hộp chữ nhật

=>ABCD;A'B'C'D' ADD'A' BCC'B' là hình chữ nhật

ABCD là hình chữ nhật nên BC//AD

=>Các vecto cùng phương với vecto BC là: \(\overrightarrow{CB};\overrightarrow{AD};\overrightarrow{DA}\)

ADD'A' là hình chữ nhật

=>AD//A'D'

=>A'D'//BC

=>Các vecto cùng phương với vecto BC là: \(\overrightarrow{A'D'};\overrightarrow{D'A'}\)

BCC'B' là hình chữ nhật

=>B'C'//BC

=>Các vecto cùng phương với vecto BC là: \(\overrightarrow{B'C'};\overrightarrow{C'B'}\)

b: Vì ABCD.A'B'C'D' là hình hộp chữ nhật nên AA'//BB'//CC'//DD'

=>Các vecto cùng hướng với vecto BB' là \(\overrightarrow{AA'};\overrightarrow{CC'};\overrightarrow{DD'}\)

d: \(\overrightarrow{CD}+\overrightarrow{BB'}=\overrightarrow{CD}+\overrightarrow{DD'}=\overrightarrow{CD'}\)

e: \(\overrightarrow{CO}-\overrightarrow{CA'}=\overrightarrow{CO}+\overrightarrow{A'C}=\overrightarrow{A'O}\)

 

i:

Gọi O' là tâm của hình bình hành A'B'C'D'

A'B'C'D' là hình bình hành

=>\(\overrightarrow{IA'}+\overrightarrow{IB'}+\overrightarrow{IC'}+\overrightarrow{ID'}=4\cdot\overrightarrow{IO'}\)