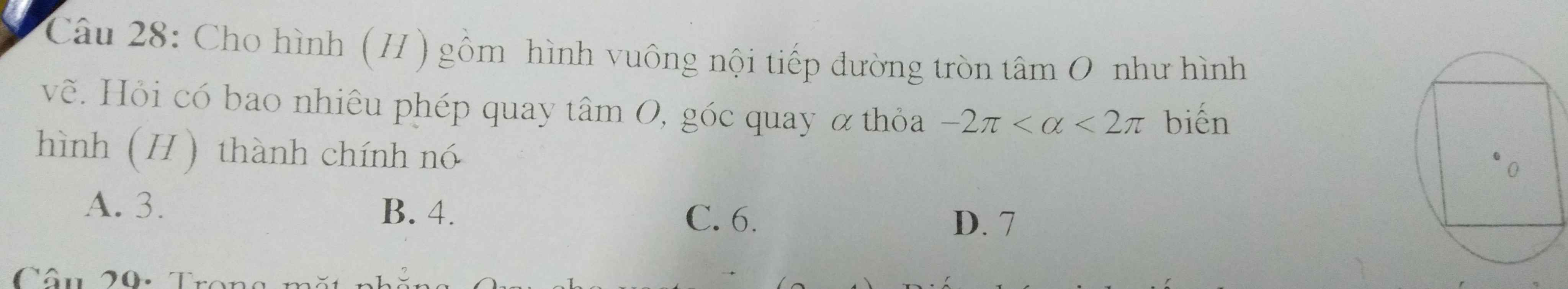Chương 1: HÀM SỐ LƯỢNG GIÁC. PHƯƠNG TRÌNH LƯỢNG GIÁC
Các câu hỏi tương tự
Tính số hình chữ nhật được tạo thành từ 4 trong 20 đỉnh của đa giác đều có 20 cạnh nội tiếp đường tròn tâm o
BÀI 1. Cho hình vuông ABCD tâm O. Hãy dựng hình vưởng A'B'C'D' là ảnh của hình vuông ABCD qua phép tỉnh tiến theo vector AO.
Cho góc \(\alpha\) thỏa mãn : \(\frac{\pi}{2}
Có bao nhiêu phép quay biến tâm giác đều tâm ở thành chính nó góc quay 0≤α≤2π. Giải thích
Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có B(-1,-2), C(6,-1) nội tiếp đường tròn tâm I(2,2) .Gọi M là trung điểm AC , H là hình chiếu của M lên AB .Tìm tọa độ của A biết rằng H thuộc đương thẳng 5x-y-1=0 và H là hoành độ dương
Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có B(-1,-2), C(6,-1) nội tiếp đường tròn tâm I(2,2) .Gọi M là trung điểm AC , H là hình chiếu của M lên AB .Tìm tọa độ của A biết rằng H thuộc đương thẳng 5x-y-1=0 và H là hoành độ dương
1.Cho alpha,betaleft(alphanebetaright)inleft(0;dfrac{pi}{2}right)và thỏa mãn điều kiện dfrac{cosx-cosalpha}{cosx-cosbeta}dfrac{sin^2alpha cosbeta}{sin^2beta cosalpha}(giả sử x xác định). Chứng minhtan^2dfrac{x}{2}tan^2dfrac{alpha}{2}tan^2dfrac{beta}{2}2. Giải hệ phương trình left{{}begin{matrix}xy-2y-3sqrt{y-x-1}+sqrt{y-3x+5}left(1-yright)sqrt{2x-y}+2left(x-1right)left(2x-y-1right)sqrt{y}end{matrix}right.3. Cho ba số thực dương a, b, c thỏa mãn dfrac{1}{a+2}+dfrac{1}{b+3}+dfrac{1}{c+4}1. Tìm Min...
Đọc tiếp
1.Cho \(\alpha,\beta\left(\alpha\ne\beta\right)\in\left(0;\dfrac{\pi}{2}\right)\)và thỏa mãn điều kiện \(\dfrac{cosx-cos\alpha}{cosx-cos\beta}=\dfrac{sin^2\alpha cos\beta}{sin^2\beta cos\alpha}\)
(giả sử \(x\) xác định). Chứng minh\(tan^2\dfrac{x}{2}=tan^2\dfrac{\alpha}{2}tan^2\dfrac{\beta}{2}\)
2. Giải hệ phương trình \(\left\{{}\begin{matrix}xy-2y-3=\sqrt{y-x-1}+\sqrt{y-3x+5}\\\left(1-y\right)\sqrt{2x-y}+2\left(x-1\right)=\left(2x-y-1\right)\sqrt{y}\end{matrix}\right.\)
3. Cho ba số thực dương a, b, c thỏa mãn \(\dfrac{1}{a+2}+\dfrac{1}{b+3}+\dfrac{1}{c+4}=1\). Tìm Min của biểu thức \(P=a+b+c+\dfrac{4}{\sqrt[3]{a\left(b+1\right)\left(c+2\right)}}+3\)
4. Tìm m để hệ bất phương trình \(\left\{{}\begin{matrix}x^2-5x+9\le\left|x-6\right|\\x^2+2x-3m^2+4\left|m\right|-4\le0\end{matrix}\right.\)
Cho \(5\sin2\alpha-6\cos\alpha=0\) và \(0< \alpha< \dfrac{\pi}{2}\)
Tính A = \(\cos(\dfrac{\pi}{2}-\alpha)+\sin\left(2017\pi-\alpha\right)-\cot(2018\pi+\alpha)\)
Phương trình : tanxtanalpha ( hằng số alphanefrac{Pi}{2}+kPi,kin Z ) có tất cả các nghiệm là :
A. xalpha+k2Pi,xPi-alpha+k2Pileft(kin Zright)
B. xalpha+kPi,x-alpha+kPileft(kin Zright)
C. xalpha+k2Pi,left(kin Zright)
D. xalpha+kPi,left(kin Zright)
Đọc tiếp
Phương trình : \(tanx=tan\alpha\) ( hằng số \(\alpha\ne\frac{\Pi}{2}+k\Pi,k\in Z\) ) có tất cả các nghiệm là :
A. \(x=\alpha+k2\Pi,x=\Pi-\alpha+k2\Pi\left(k\in Z\right)\)
B. \(x=\alpha+k\Pi,x=-\alpha+k\Pi\left(k\in Z\right)\)
C. \(x=\alpha+k2\Pi,\left(k\in Z\right)\)
D. \(x=\alpha+k\Pi,\left(k\in Z\right)\)