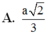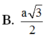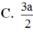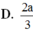Đáp án C
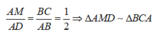
![]()
![]()
⇒ A C ⊥ D M
Vì S H ⊥ ( A B C D ) ⇒ D H ⊥ ( S A C )
từ H kẻ H K ⊥ S D
⇒ H K là khoảng cách cần tính.
Ta có D H H M = D C A M = 4 ⇔ D H D M = 4 5
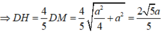
Áp dụng hệ thức lượng trong tam giác vuông.
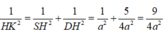
⇒ H K = 2 a 3
Đáp án C
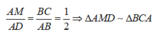
![]()
![]()
⇒ A C ⊥ D M
Vì S H ⊥ ( A B C D ) ⇒ D H ⊥ ( S A C )
từ H kẻ H K ⊥ S D
⇒ H K là khoảng cách cần tính.
Ta có D H H M = D C A M = 4 ⇔ D H D M = 4 5
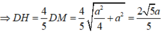
Áp dụng hệ thức lượng trong tam giác vuông.
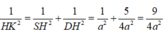
⇒ H K = 2 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD; H là giao điểm của CN với DM. Biết SH vuông góc với mặt phẳng (ABCD) và SH= a 3 . Tính khoảng cách giữa hai đường thẳng DM và SC theo a.
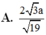
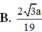
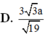
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, A D = a 3 , S A vuông góc với mặt phẳng (ABCD), góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng 60 0 . Gọi M là trung điểm của cạnh AD. Khoảng cách giữa hai đường thẳng CM và SB bằng
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với A B = a , A D = a 2 . Gọi H là trung điểm của cạnh AB. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa hai mặt phẳng (SAC) và (ABCD) là 60 ° . Tính khoảng cách giữa hai đường thẳng CH và SD
A. 2 a 5 5
B. 2 a 10 5
C. a 5 5
D. 2 a 2 5
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB=a, BC=a 2 . Tam giác SAO cân tại S, mặt phẳng (SAD) vuông góc với mặt phẳng (ABCD) góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng 60 0 . Tính khoảng cách giữa 2 đường thẳng SB và AC
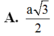
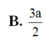
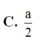
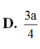
Cho hình chóp S.ABCD có đáy hình chữ nhật, AB=a; AD=2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45 0 . Gọi M là trung điểm của SD. Tính theo a khoảng cách d từ điểm M đến mặt phẳng (SAC)
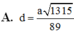
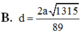
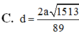
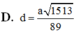
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,AB=a, AD=2a; cạnh bên SA vuông góc với mặt đáy và S A = a 5 . Khoảng cách giữa hai đường thẳng AB và SD bằng
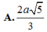
![]()
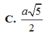
![]()
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng 60 0 . Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC.
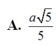
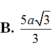
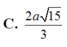
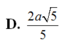
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M và N lần lượt là trung điểm của các cạnh AB và AD; H là giao điểm của CN và DM. Biết SH vuông góc với mặt phẳng (ABCD) và SH = a 3 . Tính thể tích khối chóp S.CDNM theo a.
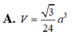
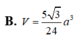
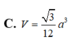
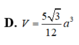
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh AB=a, BC=2a. Cạnh SA vuông góc với mặt phẳng đáy (ABCD), SA=2a. Khoảng cách giữa hai đường thẳng BD và SC bằng