Question

Cho hình chóp \(S.ABCD\) có đáy là hình thang vuông tại \(A\) và \(D\), \(SA\perp\left(ABCD\right)\) và \(SA=a\sqrt{3}\), \(AB=2AD=2CD=2a\). Gọi \(E\) là trung điểm \(AB\). Tính khoảng cách từ \(BC\) đến \(\left(SDE\right)\)?

Answer 1

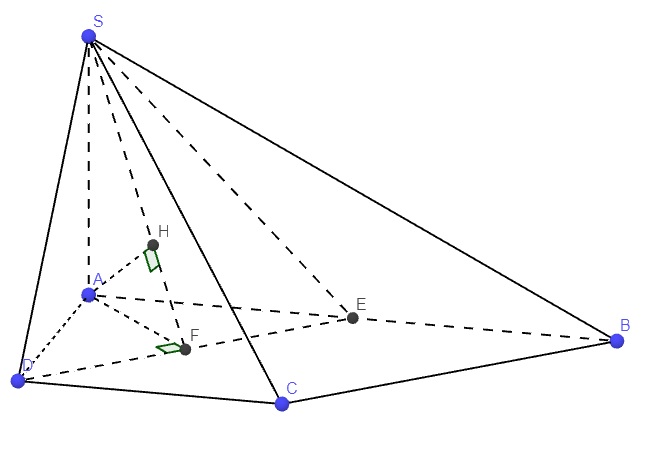
E là trung điểm AB \(\Rightarrow AE=ED=\dfrac{1}{2}AD=a\)

\(\Rightarrow BCDE\) là hình bình hành (Cặp cạnh đối BE, CD song song và bằng nhau)

\(\Rightarrow BC||DE\Rightarrow BC||\left(SDE\right)\Rightarrow d\left(BC;\left(SDE\right)\right)=d\left(B;\left(SDE\right)\right)\)

\(\left\{{}\begin{matrix}AB\cap\left(SDE\right)=E\\AE=BE\end{matrix}\right.\) \(\Rightarrow d\left(B;\left(SDE\right)\right)=d\left(A;\left(SDE\right)\right)\)

Từ A kẻ \(AF\perp DE\) (F thuộc DE), từ A kẻ \(AH\perp SF\) (H thuộc SF)

\(\Rightarrow AH\perp\left(SDE\right)\Rightarrow AH=d\left(A;\left(SDE\right)\right)=d\left(BC;\left(SDE\right)\right)\)

\(AF=\dfrac{AD.AE}{\sqrt{AD^2+AE^2}}=\dfrac{a\sqrt{2}}{2}\)

\(AH=\dfrac{SA.AF}{\sqrt{SA^2+AF^2}}=\dfrac{a\sqrt{21}}{7}\)

Answer 2