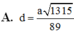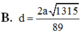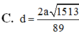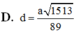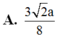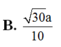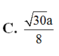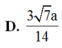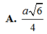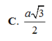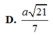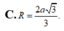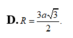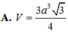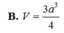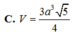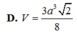Đáp án là B
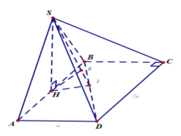
Gọi H là trung điểm của AB . Tam giác SAB đều nên suy ra SH ⊥AB . Theo giả thiết (SAB) vuông góc với ( ABCD) và có giao tuyến AB nên suy ra SH ⊥ (ABCD) tại H . Có AH ∩ (SBD) = B nên
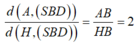
![]()
Trong ( ABCD) kẻ HI ⊥ BD tại I , kết hợp SH ⊥ (ABCD) ta suy ra
BD⊥ (SHI) => (SHI) ⊥ (SBD) , mà (SHI ) ∩ (SBD) = SI nên trong (SHI) nếu ta kẻ HK ⊥ SI tại K thì HK ⊥ (SBD) tại K , do đó HK = d (H,( SBD)) .
Ta tính được :
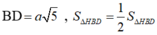
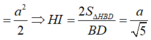
Tam giác SAB đều cạnh 2a nên SH=a 3
Tam giác SHI vuông tại H đường cao HK nên
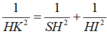
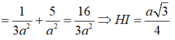
Vậy khoảng cách từ A đến (SBD) là: a 3 2