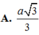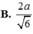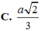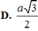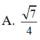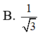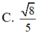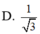Question

Cho hình chóp SABCD có ABCD là hình thoi cạnh a, tâm O và BAD  60 độ. Biết SO vuông góc mặt phẳng (ABCD), SB = 2a. a) Chứng minh AC vuông góc mp(SBD) b) Xác định và tính số đo góc giữa đường thẳng SD và mp(ABCD)

Answer 1

a: Ta có: AC\(\perp\)BD(ABCD là hình thoi)
AC\(\perp\)SO(SO\(\perp\)(ABCD))

BD,SO cùng thuộc mp(SBD)

Do đó: AC\(\perp\)(SBD)

b: \(\widehat{SD;\left(ABCD\right)}=\widehat{DS;DO}=\widehat{SDO}\)

Xét ΔABD có AB=AD và \(\widehat{BAD}=60^0\)

nên ΔABD đều

=>BD=AB=a

=>\(DO=OB=\dfrac{a}{2}=0,5a\)

Ta có: ΔSOB vuông tại O

=>\(SO^2+OB^2=SB^2\)

=>\(SO^2+\left(0,5a\right)^2=\left(2a\right)^2\)

=>\(SO^2=4a^2-0,25a^2=3,75a^2\)

=>\(SO=\dfrac{a\sqrt{15}}{2}\)

Xét ΔSOD vuông tại O có \(tanSDO=\dfrac{OS}{OD}=\dfrac{a\sqrt{15}}{2}:\dfrac{a}{2}=\sqrt{15}\)

=>\(\widehat{SDO}\simeq75^031'\)

=>\(\widehat{SD;\left(ABCD\right)}\simeq75^031'\)