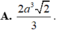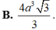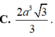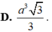Question

cho hình chóp đều SABCD có chiều cao bằng \(\sqrt{2}\) và độ dài cạnh bên bằng \(\sqrt{6}\). tính thể tích khối chóp SABCD ( tính kết quả đến hàng phần mười)

Answer 1

Gọi O là tâm của hình vuông ABCD

=>OA=OB=OC=OD

Vì S.ABCD là hình chóp đều nên SA=SB=SC=SD

mà OA=OB=OC=OD

nên SO⊥(ABCD)

=>\(SO=\sqrt2\)

ΔSOA vuông tại O

=>\(SA^2=SO^2+OA^2\)

=>\(OA^2=\left(\sqrt6\right)^2-\left(\sqrt2\right)^2=6-2=4=2^2\)

=>OA=2(cm)

=>\(AC=2\cdot2=4\left(\operatorname{cm}\right)\)

ΔABC vuông tại B

=>\(BA^2+BC^2=AC^2\)

=>\(2\cdot BA^2=4^2=16\)

=>\(BA^2=8=\left(2\sqrt2\right)^2\)

=>\(BA=2\sqrt2\left(\operatorname{cm}\right)\)

ABCD là hình vuông

=>\(S_{đáy}=BA^2=\left(2\sqrt2\right)^2=8\)

=>\(V=\frac13\cdot8\cdot\sqrt2=\frac{8\sqrt2}{3}\left(\operatorname{cm}^2\right)\)