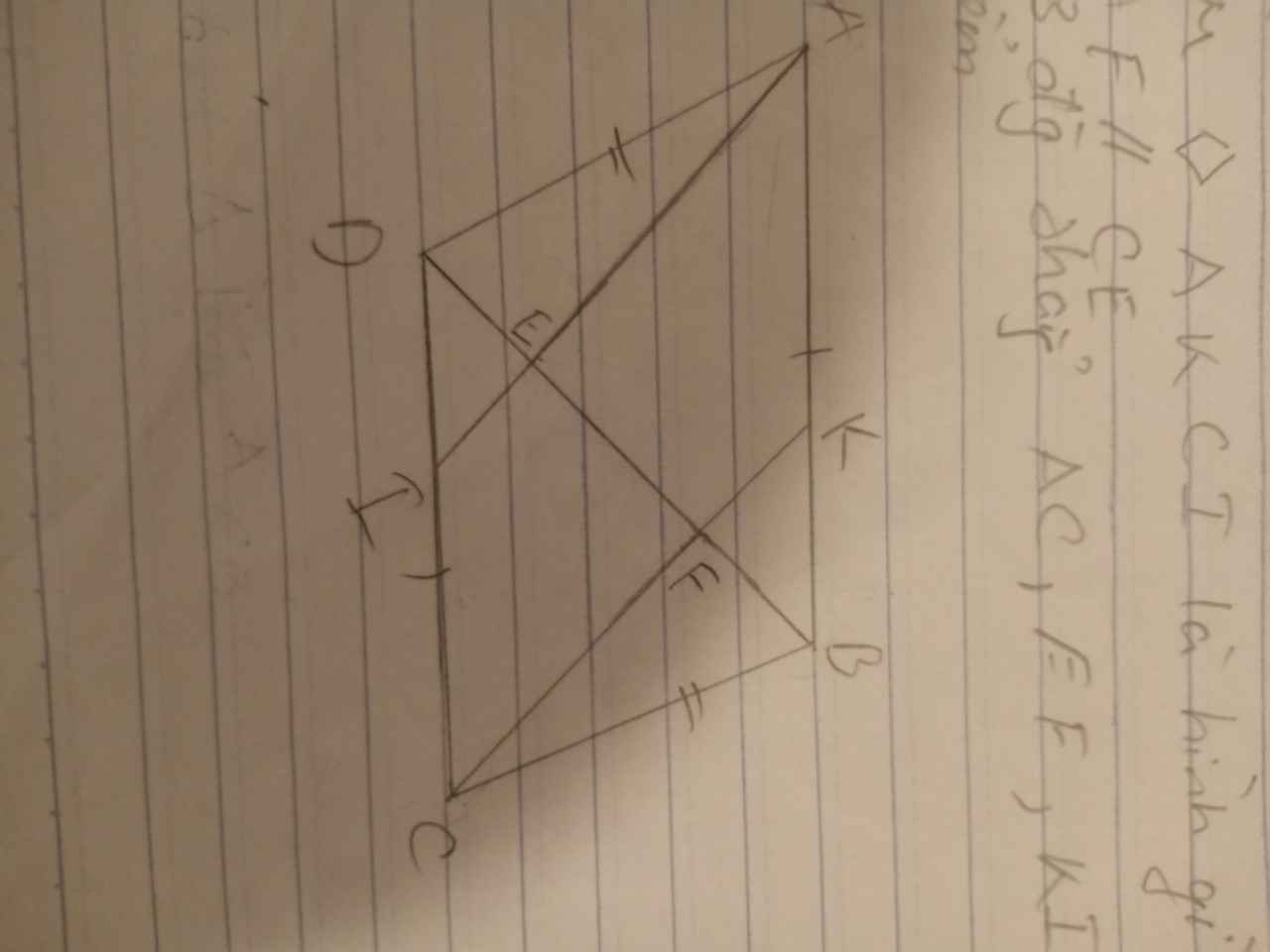
a) Vì ABCD là hình bình hành \(\left(gt\right)\)
\(\Rightarrow\left\{{}\begin{matrix}AD//BC\\AD=BC\end{matrix}\right.\)\(\left(t/c\right)\)
Vì \(\left\{{}\begin{matrix}AI\perp BD\\CK\perp BD\end{matrix}\right.\)\(\left(gt\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{AID}=\widehat{BKC}=90^o\\AI//CK\end{matrix}\right.\)
Vì \(AD//BC\left(cmt\right)\Rightarrow\widehat{ADI}=\widehat{CBK}\) (2 góc so le trong)
Xét \(\Delta AID\) và \(\Delta CKB\) có:
\(\widehat{AID}=\widehat{BKC}=90^o\left(cmt\right)\)
\(AD=BC\left(cmt\right)\)
\(\widehat{ADI}=\widehat{CBK}\left(cmt\right)\)
Nên \(\Delta AID=\Delta CKB\) (ch-gn)
\(\Rightarrow AI=CK\) (2 cạnh tương ứng)
Xét tứ giác AICK có \(\left\{{}\begin{matrix}AI//CK\left(cmt\right)\\AI=CK\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\) AICK là hình bình hành (dhnb)
b) Vì \(AI//CK\left(cma\right)\Leftrightarrow AM//CN\)
Vì ABCD là hình bình hành \(\left(gt\right)\)
\(\Rightarrow AB//CD\Leftrightarrow AN//CM\)
Xét tứ giác AMCN có \(\left\{{}\begin{matrix}AM//CN\left(cmt\right)\\AN//CM\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\) AMCN là hình bình hành (dhnb).