Các câu hỏi tương tự
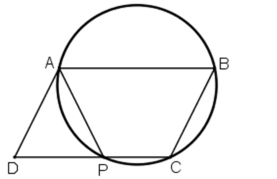
Cho hình bình hành ABCD. Đường tròn đi qua ba đỉnh A, B, C cắt đường thẳng CD tại P khác C. Chứng minh AP = AD.
cho hình bình hành ABCD , Đường tròn đi qua ba đình Ạ , B , C cắt đường thẳng CD tại P ( P khác C ) . chứng minh rằng AP=AD .
Cho hình bình hành ABCD với AB < AD biết rằng đường tròn đi qua 3 điểm a b c cắt tại CD tại điểm E Chứng minh AD = Ae
Cho hình bình hành ABCD , Đường tròn đi qua ba đình Ạ , B , C cắt đường thẳng CD tại P ( P khác C ) . Chứng minh rằng AP=AD .
Cho hình bình hành ABCD với góc BAD < 90 độ. Đường phân giác của góc BCD cắt đường tròn ngoại tiếp tam giác BCD tại O khác C. kẻ đường thẳng d đi qua A và vuông góc với CO. Đường thẳng d lần lượt cắt các đường thẳng CB, CD tại E và F. Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác CEF.
Cho tam giác ABC cân tại A, nội tiếp đường tròn tâm O. Vẽ hình bình hành ABCD. Tiếp tuyến tại C của đường tròn cắt đường thẳng AD tại N. Chứng minh:
a, Đường thẳng AD là tiếp tuyến của (O)
b, Ba đường thẳng AC, BD và ON đồng quy
Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Vẽ hình bình hành ABCD. Tiếp tuyến tại C của đường tròn cắt AD tại N. Chứng minh rằng :
a) AD là tiếp tuyến của đường tròn
b) Ba đường thẳng AC, BD,ON đồng quy
Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Vẽ hình bình hành ABCD. Tiếp tuyến tại C của đường tròn cắt AD tại N. Chứng minh rằng :
a) AD là tiếp tuyến của đường tròn
b) Ba đường thẳng AC, BD,ON đồng quy
Cho hình bình hành ABCD. Một đường thẳng d đi qua A cắt BD tại P, cắt các đường thẳng BC và CD lần lượt tại M và N. Chứng minh:
a) BM x DN không đổi
b) \(\frac{1}{AM}+\frac{1}{AN}=\frac{1}{AP}\)